题目内容
13.在△ABC中,AB=AC,点D在BC边所在的直线上,过点D作DE∥AC交直线AB于E,DF∥AB交直线AC于点F,当点D在边BC上时,如图①,此时DE、DF、AC满足DE+DF=AC.(1)当点D在BC的延长线或方向延长线上时,如图②、如图③,此时,DE、DF、AC分别存在怎样的数量关系?请写出来,并选择一个加以证明.
(2)若AC=6,DE=4,则DF=2.

分析 (1)证明四边形AFDE是平行四边形,且△DCF和△BDF是等腰三角形即可证得;
(2)根据(1)中的结论代入数据直接求解.
解答 解:(1)图②③中:AC+DF=DE.
证明:图②结论:
∵DE∥AC,DF∥AB,
∴四边形AEDF是平行四边形,
∴AF=DE.
∵DE∥AC,
∴∠CDF=∠B,
又∵AB=AC,
∴∠B=∠ACB,
∴∠CDF=∠ACB,
∵∠ACB=∠DCF,
∴∠CDF=∠DCF,
∴DF=CF,
∴AC+DF=AF=DE;
同理可证出图③结论:AC+DF=AF=DE.
(2)当如图①的情况,DF=AC-DE=6-4=2;
当如图②③的情况,DF=DE-AC=4-6=-2(舍去).
故答案为:2.
点评 本题考查了平行线的性质、等腰三角形的性质依据平行线的判定及性质,解题的关键是:(1)证出AC+DF=AF=DE;(2)代入数据直接求解.本题属于中档题,难度不大,解决该题型题目时,根据平行四边形的判定即性质找出相等的边角关系是关键.

练习册系列答案
相关题目
4.若分式$\frac{2x+y}{xy}$中,x、y的值都扩大3倍,则原分式的值( )
| A. | 扩大3倍 | B. | 缩小3倍 | C. | 不变 | D. | 无法确定 |
2.下列方程中,是一元二次方程的是( )
| A. | x2+2x-4=0 | B. | 6x2+2=6x2-x | C. | -3x+2=0 | D. | x2+2xy-3y2=0 |
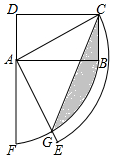 如图矩形ABCD中,AD=1,CD=$\sqrt{3}$,连接AC,将线段AC、AB分别绕点A顺时针旋转90°至AE、AF,线段AE与弧BF交于点G,连接CG,则图中阴影部分面积为$\frac{π}{2}$-$\frac{\sqrt{3}}{2}$.
如图矩形ABCD中,AD=1,CD=$\sqrt{3}$,连接AC,将线段AC、AB分别绕点A顺时针旋转90°至AE、AF,线段AE与弧BF交于点G,连接CG,则图中阴影部分面积为$\frac{π}{2}$-$\frac{\sqrt{3}}{2}$. (1)请在横线上填写合适的内容,完成下面的证明:
(1)请在横线上填写合适的内容,完成下面的证明: