题目内容
20．观察下列各式：a+b=1，a2+b2=3，a3+b3=4，a4+b4=7，a5+b5=11，…，则a12+b12=322．分析 根据题目中式子，可以发现其中的规律，从而可以解答本题．
解答 解：∵a+b=1，a2+b2=3，a3+b3=4，a4+b4=7，a5+b5=11，…，
∴a6+b6=11+7=18，a7+b7=18+11=29，a8+b8=29+18=47，a9+b9=47+29=76，a10+b10=76+47=123，a11+b11=123+76=199，a12+b12=199+123=322，
∴a12+b12=322，
故答案为：
点评 本题考查数字的变化类，解题的关键是明确题意，找出数字的变化规律．
练习册系列答案
相关题目
11．对于两数a、b，定义运算：a*b=a+b-ab，则在下列等式中，正确的为（ ）
①a*2=2*a ②（-2）*a=a*（-2）③（2*a）*3=2*（a*3）④0*a=a．
①a*2=2*a ②（-2）*a=a*（-2）③（2*a）*3=2*（a*3）④0*a=a．
| A． | ①③ | B． | ①②③ | C． | ①②③④ | D． | ①②④ |
8．
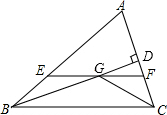如图，在△ABC中，∠ABC和∠ACB的平分线相交于点G，过点G作EF∥BC交AB于E，交AC于F，过点G作GD⊥AC于D，下列四个结论：
①EF=BE+CF；
②∠BGC=90°+$\frac{1}{2}$∠A；
③点G到△ABC各边的距离相等；
④设GD=m，AE+AF=n，则S△AEF=mn．
其中正确的结论有（ ）
如图，在△ABC中，∠ABC和∠ACB的平分线相交于点G，过点G作EF∥BC交AB于E，交AC于F，过点G作GD⊥AC于D，下列四个结论：①EF=BE+CF；
②∠BGC=90°+$\frac{1}{2}$∠A；
③点G到△ABC各边的距离相等；
④设GD=m，AE+AF=n，则S△AEF=mn．
其中正确的结论有（ ）
| A． | ①②④ | B． | ①③④ | C． | ①②③ | D． | ①②③④ |
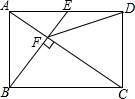如图，在矩形ABCD中，E是AD边的中点，BE⊥AC于点，连接DF，分析下列五个结论：①△AEF∽△CAB；②CF=2AF；③DF=DC；④tan∠ACD=$\sqrt{2}$；⑤S四边形CDEF=$\frac{5}{2}{S_{△ABF}}$其中正确的结论有（ ）