题目内容
8.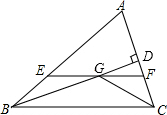 如图,在△ABC中,∠ABC和∠ACB的平分线相交于点G,过点G作EF∥BC交AB于E,交AC于F,过点G作GD⊥AC于D,下列四个结论:
如图,在△ABC中,∠ABC和∠ACB的平分线相交于点G,过点G作EF∥BC交AB于E,交AC于F,过点G作GD⊥AC于D,下列四个结论:①EF=BE+CF;
②∠BGC=90°+$\frac{1}{2}$∠A;
③点G到△ABC各边的距离相等;
④设GD=m,AE+AF=n,则S△AEF=mn.
其中正确的结论有( )
| A. | ①②④ | B. | ①③④ | C. | ①②③ | D. | ①②③④ |
分析 ①根据∠ABC和∠ACB的平分线相交于点G可得出∠EBG=∠CBG,∠BCG=∠FCG,再由EF∥BC可知∠CBG=∠EGB,∠BCG=∠CGF,故可得出BE=EG,GF=CF,由此可得出结论;
②先根据角平分线的性质得出∠GBC+∠GCB=$\frac{1}{2}$(∠ABC+∠ACB),再由三角形内角和定理即可得出结论;
③根据三角形内心的性质即可得出结论;
④连接AG,根据三角形的面积公式即可得出结论.
解答 解:①∵∠ABC和∠ACB的平分线相交于点G,
∴∠EBG=∠CBG,∠BCG=∠FCG.
∵EF∥BC,
∴∠CBG=∠EGB,∠BCG=∠CGF,
∴∠EBG=∠EGB,∠FCG=∠CGF,
∴BE=EG,GF=CF,
∴EF=EG+GF=BE+CF,故本小题正确;
②∵∠ABC和∠ACB的平分线相交于点G,
∴∠GBC+∠GCB=$\frac{1}{2}$(∠ABC+∠ACB)=$\frac{1}{2}$(180°-∠A),
∴∠BGC=180°-(∠GBC+∠GCB)=180°-$\frac{1}{2}$(180°-∠A)=90°+$\frac{1}{2}$∠A,故本小题正确;
③∵∠ABC和∠ACB的平分线相交于点G,
∴点G是△ABC的内心,
∴点G到△ABC各边的距离相等,故本小题正确;
④连接AG,
∵点G是△ABC的内心,GD=m,AE+AF=n,
∴S△AEF=$\frac{1}{2}$AE•GD+$\frac{1}{2}$AF•GD=$\frac{1}{2}$(AE+AF)•GD=$\frac{1}{2}$nm,故本小题错误.
故选C
点评 本题考查的是等腰三角形的判定与性质,熟知角平分线的性质、三角形内角和定理及三角形内心的性质是解答此题的关键.

练习册系列答案
 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案
相关题目
18.(2a2b-3c-1)-2的结果是( )
| A. | -4a-4b6c2 | B. | $\frac{1}{4}{a^{-4}}{b^{-5}}{c^{-3}}$ | C. | $\frac{{{b^6}{c^2}}}{{4{a^4}}}$ | D. | $\frac{{4{a^4}}}{{{b^6}{c^2}}}$ |
3.四边形ABCD内接于⊙O,$\widehat{AB}$:$\widehat{BC}$:$\widehat{CD}$=2:3:5,∠BAD=120°,则∠ABC的度数为( )
| A. | 100° | B. | 105° | C. | 120° | D. | 125° |
13.下列四个数中最大的是( )
| A. | -2 | B. | 0 | C. | -$\frac{3}{5}$ | D. | 0.7 |
17.△ABC与△DEF的相似比为1:4,则△DEF与△ABC的相似比为( )
| A. | 1:2 | B. | 1:3 | C. | 4:1 | D. | 1:16 |
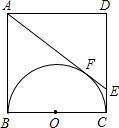 如图,已知正方形ABCD的边长为4cm,以BC为直径作半圆O,AE与半圆相切于点F,交CD于E,则△ADE的面积为6cm2.
如图,已知正方形ABCD的边长为4cm,以BC为直径作半圆O,AE与半圆相切于点F,交CD于E,则△ADE的面积为6cm2.