题目内容

20．如图，将矩形ABCD绕点A顺时针旋转到AB′C′D′的位置，旋转角为α（0°＜α＜90°）．若∠1=120°，则∠α=30°．

分析 根据对顶角相等求出∠2，再根据四边形的内角和等于360°求出∠BAD′，然后求出∠DAD′，最后根据旋转的性质可得∠DAD′即为旋转角．

解答 解：如图，由对顶角相等得，∠2=∠1=120°，
在四边形中，∠BAD′=360°-90°×2-∠2=360°-180°-120°=60°，
所以，∠DAD′=90°-60°=30°，
即旋转角∠α=∠DAD′=30°．
故答案为：30°．

点评 本题考查了旋转的性质，四边形的内角和定理，对顶角相等的性质，熟记性质并考虑利用四边形的内角和定理求解是解题的关键．

练习册系列答案
相关题目
6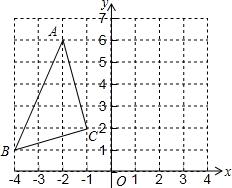．如图，在平面直角坐标系中，△ABC的顶点都在方格纸的格点上，如果将△ABC先向右平移4个单位长度，再向下平移1个单位长度，得到△A1B1C1，那么点A的对应点A1的坐标为（　　）
A．（4，3）B．（2，4）C．（3，1）D．（2，5）
7．小亮上周每天的睡眠时间为（单位：小时）：8，9，10，7，10，9，9，这组数据的众数是9．
8．如图，在平面直角坐标系中，矩形ABCO的面积为60，边OA比边OC大4，E为BC的中点，以OE为直径的⊙O′交x轴于D点，过D点作DF⊥AE于F．
（1）求OA，OC的长；
（2）求证：DF为⊙O′的切线；
（3）若点P从点C出发以每秒2个单位的速度沿着射线CB运动，则运动t秒后，使得点P、O、A构成以OA为腰的等腰三角形．
①求t的值；
②当点P、O、A构成以OA为腰的等腰三角形时，直接写出点P与以O为圆心OA长为半径的圆的位置关系．
15．如图，直线l上摆放着两块大小相同的直角三角板，它们中较长直角边的长为$\sqrt{3}$cm，较小锐角的度数为30°．

（1）将△ECD沿直线AC翻折到如图（a）的位置，ED′与AB相交于点F，则BD′=$\sqrt{3}$-1cm，∠BFD′=30度．
（2）将△ECD沿直线l向左平移到（b）的位置，使E点落在AB上，则平移的距离是1-$\frac{\sqrt{3}}{3}$cm．
（3）将△ECD绕点C逆时针方向旋转得到△E′C D′，设DE与C D′的交点为M，若△CDM为等腰三角形，则旋转角为30°或75°．（0°＜旋转角＜180°）
5．如图①，在正方形ABCD中，点P沿边DA从点D开始向点A以2cm/s的速度移动；同时，点Q沿边AB、BC从点A开始向点C以3cm/s的速度移动．当点P移动到点A时，P、Q同时停止移动．设点P出发x s时，△PAQ的面积为ycm2，y与x的函数图象如图2所示，则线段EF所在的直线对应的函数关系式为y=-6x+18（2≤x＜3）．
12．计算：2-1+$\sqrt{2}$•tan45°-（π-2015）0．
9．-（+2）的相反数等于（　　）
A．2B．-2C．±2D．±$\frac{1}{2}$
10．如图，MN表示一段笔直的高架道路，线段AB表示高架道路旁的一排居民楼，已知点A到MN的距离为15米，BA的延长线与MN相交于点D，且∠BDN=30°，假设汽车在高速道路上行驶时，周围39米以内会受到噪音的影响．
（1）过点A作MN的垂线，垂足为点H，如果汽车沿着从M到N的方向在MN上行驶，当汽车到达点P处时，噪音开始影响这一排的居民楼，那么此时汽车与点H的距离为多少米？
（2）降低噪音的一种方法是在高架道路旁安装隔音板，当汽车行驶到点Q时，它与这一排居民楼的距离QC为39米，那么对于这一排居民楼，高架道路旁安装的隔音板至少需要多少米长？（精确到1米）（参考数据：$\sqrt{3}$≈1.7）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网