题目内容
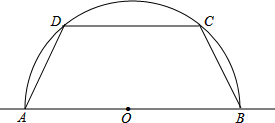 已知半圆O中,直径AB=2,作弦DC∥AB,设AD=x,四边形ABCD的周长为y,求:y与x的函数关系式,并写出自变量x的取值范围.
已知半圆O中,直径AB=2,作弦DC∥AB,设AD=x,四边形ABCD的周长为y,求:y与x的函数关系式,并写出自变量x的取值范围.考点:垂径定理,勾股定理
专题:
分析:连接BD,过D作DE⊥AB于E,过C作CF⊥AB于F,设CD=a,由平行得到弧AD=弧BC,推出AD=BC,得出矩形CDEF,根据矩形的性质推出CD=EF,证△CFB≌△DEA,求出AEBF=
,根据勾股定理求出BD,DE,关键三角形的面积公式求得a的值,则梯形的周长可以求得,即可得到y与x的函数关系式.
| 2-a |
| 2 |
解答: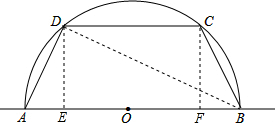 解:连接BD,过D作DE⊥AB于E,过C作CF⊥AB于F,设CD=a,
解:连接BD,过D作DE⊥AB于E,过C作CF⊥AB于F,设CD=a,
∵CD∥AB,
∴弧AD=弧BC,
∴AD=BC,
∴四边形CDEF是矩形,
∴CD=EF,
在直角△CFB和直角△DEA中,
∴△CFB≌△DEA(HL),
∴AE=BF=
,
在△ADB中由勾股定理得:BD=
=
,
在△AED中由勾股定理得DE=
=
,
根据三角形的面积公式得:
×2×
=
×x×
,
解得:a=2+x2(舍去),a=2-x2,
y与x的函数关系式为:y=2+x+x+2-x2=-x2+2x+4.即y=-x2+2x+4(0<x<
).
 解:连接BD,过D作DE⊥AB于E,过C作CF⊥AB于F,设CD=a,
解:连接BD,过D作DE⊥AB于E,过C作CF⊥AB于F,设CD=a,∵CD∥AB,
∴弧AD=弧BC,
∴AD=BC,
∴四边形CDEF是矩形,
∴CD=EF,
在直角△CFB和直角△DEA中,
|
∴△CFB≌△DEA(HL),
∴AE=BF=
| 2-a |
| 2 |
在△ADB中由勾股定理得:BD=
| AB2-AD2 |
| 4-x2 |
在△AED中由勾股定理得DE=
| AD2-AE2 |
x2-
|
根据三角形的面积公式得:
| 1 |
| 2 |
x2-
|
| 1 |
| 2 |
| 4-x2 |
解得:a=2+x2(舍去),a=2-x2,
y与x的函数关系式为:y=2+x+x+2-x2=-x2+2x+4.即y=-x2+2x+4(0<x<
| 2 |
点评:本题主要考查对勾股定理,矩形的性质和判定,全等三角形的性质和判定,三角形的面积,圆心角,弧,弦之间的关系,等腰梯形的性质,平行线的性质,能综合运用这些性质进行计算是解此题的关键.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
 ⊙O1与⊙O2外切于点P,过P点的直线AB与⊙O1和⊙O2相交于A、B,⊙O1的切线AD与⊙O2相交于点C、D.求证:
⊙O1与⊙O2外切于点P,过P点的直线AB与⊙O1和⊙O2相交于A、B,⊙O1的切线AD与⊙O2相交于点C、D.求证:
 矩形ABCD的对角线相交于点O,DE∥AC,CE∥DB,CE、DE交于点E,证明:四边形DOCE是菱形.
矩形ABCD的对角线相交于点O,DE∥AC,CE∥DB,CE、DE交于点E,证明:四边形DOCE是菱形.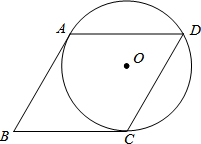 如图,⊙O经过菱形ABCD的三个顶点A、C、D,且∠B=60°.
如图,⊙O经过菱形ABCD的三个顶点A、C、D,且∠B=60°.
 如图,点E在△ABC外部,点D在BC边上,DE交AC于点F,若∠1=∠2=∠3,AC=AE,求证:AB=AD.
如图,点E在△ABC外部,点D在BC边上,DE交AC于点F,若∠1=∠2=∠3,AC=AE,求证:AB=AD.