题目内容
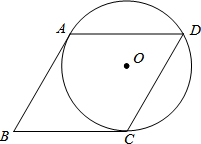 如图,⊙O经过菱形ABCD的三个顶点A、C、D,且∠B=60°.
如图,⊙O经过菱形ABCD的三个顶点A、C、D,且∠B=60°.(1)求证:AB为⊙O的切线;
(2)若⊙O的半径为1,求菱形ABCD的面积.
考点:切线的判定,菱形的性质
专题:证明题
分析:(1)连接OA、OB、OC,如图,根据菱形的性质得BA=BC,∠D=∠ABC=60°,则利用圆周角定理得∠AOC=2∠D=120°,再根据“SSS”判断△OBA≌△OBC,得到∠1=∠2,∠3=∠4,所以∠1=
∠ABC=30°,∠3=
∠AOC=60°,于是可计算出∠OAB=90,然后根据切线的判定定理可得AB为⊙O的切线;
(2)作AM⊥BC于点M,如图,根据含30度的直角三角形三边的关系,在Rt△OAB中计算出AB=
OA=
,在Rt△ABM中计算出BM=
AB=
,AM=
BM=
,
然后根据菱形的面积公式求解.
| 1 |
| 2 |
| 1 |
| 2 |
(2)作AM⊥BC于点M,如图,根据含30度的直角三角形三边的关系,在Rt△OAB中计算出AB=
| 3 |
| 3 |
| 1 |
| 2 |
| ||
| 2 |
| 3 |
| 3 |
| 2 |
然后根据菱形的面积公式求解.
解答:(1)证明:连接OA、OB、OC,如图,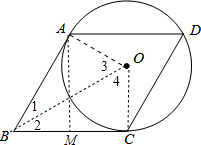
∵四边形ABCD是菱形,
∴BA=BC,∠D=∠ABC=60°,
∴∠AOC=2∠D=120°,
在△OBA和△OBC中
,
∴△OBA≌△OBC,
∴∠1=∠2,∠3=∠4,
∴∠1=
∠ABC=30°,∠3=
∠AOC=60°,
∴∠OAB=180°-∠1-∠3=90,
∴OA⊥AB,
∴AB为⊙O的切线;
(2)解:作AM⊥BC于点M,如图,
⊙O的半径为1,即OA=1,
在Rt△OAB中,∵∠1=30°,
∴AB=
OA=
,
在Rt△ABM中,∵∠BAM=30°,
∴BM=
AB=
,
∴AM=
BM=
,
∵BC=AB=
,
∴S菱形ABCD=
•
=
.

∵四边形ABCD是菱形,
∴BA=BC,∠D=∠ABC=60°,
∴∠AOC=2∠D=120°,
在△OBA和△OBC中
|
∴△OBA≌△OBC,
∴∠1=∠2,∠3=∠4,
∴∠1=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠OAB=180°-∠1-∠3=90,
∴OA⊥AB,
∴AB为⊙O的切线;
(2)解:作AM⊥BC于点M,如图,
⊙O的半径为1,即OA=1,
在Rt△OAB中,∵∠1=30°,
∴AB=
| 3 |
| 3 |
在Rt△ABM中,∵∠BAM=30°,
∴BM=
| 1 |
| 2 |
| ||
| 2 |
∴AM=
| 3 |
| 3 |
| 2 |
∵BC=AB=
| 3 |
∴S菱形ABCD=
| 3 |
| 2 |
| 3 |
3
| ||
| 2 |
点评:本题考查了切线的判定定理:经过半径的外端且垂直于这条半径的直线是圆的切线.也考查了菱形的性质和含30度的直角三角形三边的关系.

练习册系列答案
 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案
相关题目
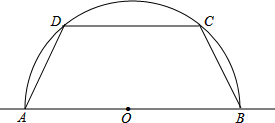 已知半圆O中,直径AB=2,作弦DC∥AB,设AD=x,四边形ABCD的周长为y,求:y与x的函数关系式,并写出自变量x的取值范围.
已知半圆O中,直径AB=2,作弦DC∥AB,设AD=x,四边形ABCD的周长为y,求:y与x的函数关系式,并写出自变量x的取值范围. 如图所示,AD=AE,BE=CD,∠1=∠2,除了△ABD与△ACE,图中还有其他的全等三角形吗?请找出来并加以证明.
如图所示,AD=AE,BE=CD,∠1=∠2,除了△ABD与△ACE,图中还有其他的全等三角形吗?请找出来并加以证明.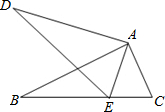 如图,在△ABC和△ADE中,点E在BC上,∠BAC=∠DAE,∠B=∠D,AB=AD,
如图,在△ABC和△ADE中,点E在BC上,∠BAC=∠DAE,∠B=∠D,AB=AD,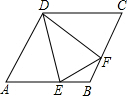 已知如图,在菱形ABCD中,EF分别是AB和BC上的点,且BE=BF,求证:
已知如图,在菱形ABCD中,EF分别是AB和BC上的点,且BE=BF,求证: