题目内容
 ⊙O1与⊙O2外切于点P,过P点的直线AB与⊙O1和⊙O2相交于A、B,⊙O1的切线AD与⊙O2相交于点C、D.求证:
⊙O1与⊙O2外切于点P,过P点的直线AB与⊙O1和⊙O2相交于A、B,⊙O1的切线AD与⊙O2相交于点C、D.求证: |
| BC |
 |
| BD |
考点:切线的性质,相切两圆的性质
专题:证明题
分析:如图,过点P作两圆的公切线MN.欲证明
=
,需要推知∠BDC=∠BCD.
 |
| BC |
 |
| BD |
解答: 证明:如图,过点P作两圆的公切线MN.连接BD、PD、CB.
证明:如图,过点P作两圆的公切线MN.连接BD、PD、CB.
∵AD,⊙O1的切线,MN是公切线,
∴∠1=∠2=∠3=∠6.
∵∠4=∠5,∠BDC=∠5+∠6,∠BCD=∠1+∠4,
∴∠BDC=∠BCD,
∴
=
.
 证明:如图,过点P作两圆的公切线MN.连接BD、PD、CB.
证明:如图,过点P作两圆的公切线MN.连接BD、PD、CB.∵AD,⊙O1的切线,MN是公切线,
∴∠1=∠2=∠3=∠6.
∵∠4=∠5,∠BDC=∠5+∠6,∠BCD=∠1+∠4,
∴∠BDC=∠BCD,
∴
 |
| BC |
 |
| BD |
点评:本题考查了切线的性质和相切两圆的性质.此题利用了圆周角定理,圆心角、弧、弦间的关系以及弦切角定理进行解题的.

练习册系列答案
相关题目
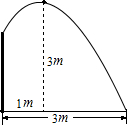 要修建一个圆形水池,在池中心竖直安装一根水管,在水管的顶端安装一个喷水头,使喷出的抛物线形水柱在与池中心的水平距离为1m处达到最高,高度为3m,水柱落地处离地中心3m.
要修建一个圆形水池,在池中心竖直安装一根水管,在水管的顶端安装一个喷水头,使喷出的抛物线形水柱在与池中心的水平距离为1m处达到最高,高度为3m,水柱落地处离地中心3m.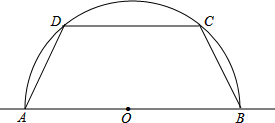 已知半圆O中,直径AB=2,作弦DC∥AB,设AD=x,四边形ABCD的周长为y,求:y与x的函数关系式,并写出自变量x的取值范围.
已知半圆O中,直径AB=2,作弦DC∥AB,设AD=x,四边形ABCD的周长为y,求:y与x的函数关系式,并写出自变量x的取值范围.