题目内容
如图，点E在△ABC外部，点D在BC边上，DE交AC于点F，若∠1=∠2=∠3，AC=AE，求证：AB=AD．考点：全等三角形的判定与性质
专题：证明题
分析：由∠2=∠3推出∠E=∠C，由∠1=∠2推出∠BAC=∠DAE，根据AAS证△ABC≌△ADE即可
解答：证明：∵∠1=∠2，
∴∠1+∠DAF=∠2+∠DAF，
即∠BAC=∠DAE，
∵∠2=∠3，∠AFE=∠DFC，
∴∠E=∠C，
在△ABC与△ADE中，
，
∴△ABC≌△ADE（AAS），
∴AB=AD．
∴∠1+∠DAF=∠2+∠DAF，
即∠BAC=∠DAE，
∵∠2=∠3，∠AFE=∠DFC，
∴∠E=∠C，
在△ABC与△ADE中，
|
∴△ABC≌△ADE（AAS），
∴AB=AD．
点评：本题考查了全等三角形的性质和判定的应用，关键是推出证明△ABC和△ADE全等的三个条件，题目比较典型，难度适中．
练习册系列答案
相关题目
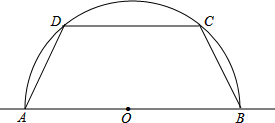已知半圆O中，直径AB=2，作弦DC∥AB，设AD=x，四边形ABCD的周长为y，求：y与x的函数关系式，并写出自变量x的取值范围．
如图，已知△ABC中，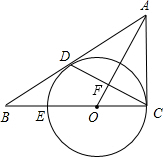
如图，△ABC中，∠ACB=90°，D是边AB上的一点，E是BC上的一点，以EC为直径的⊙O经过点D，OA⊥CD于点F．
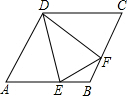已知如图，在菱形ABCD中，EF分别是AB和BC上的点，且BE=BF，求证：