题目内容
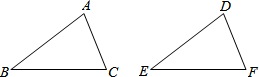
 已知,如图,E在直线DF上,B在直线AC上,若∠AGB=∠EHF,∠C=∠D.求证:AC∥DF.(注明理由)
已知,如图,E在直线DF上,B在直线AC上,若∠AGB=∠EHF,∠C=∠D.求证:AC∥DF.(注明理由)考点:平行线的判定与性质
专题:证明题
分析:首先证明BD∥EC,根据平行线的性质以及已知条件证明∠C=∠HEF,然后根据三角形的内角和定理证明∠A=∠F,从而证明直线平行.
解答:
证明:∵∠AGB=∠EHF,∠AHC=∠EHF,
∴∠AGB=∠AHC,
∴BD∥EC,
∴∠HEF=∠D,
又∵∠C=∠D,
∴∠C=∠HEF,
又∵在△ACH和△FEH中,∠AHC=∠EHF,
∴∠A=∠F,
∴AC∥DF.
∴∠AGB=∠AHC,
∴BD∥EC,
∴∠HEF=∠D,
又∵∠C=∠D,
∴∠C=∠HEF,
又∵在△ACH和△FEH中,∠AHC=∠EHF,
∴∠A=∠F,
∴AC∥DF.
点评:本题考查了平行线的判定与性质,正确证明∠C=∠HEF是解决本题的关键.

练习册系列答案
 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案
相关题目
下列各组数中,互为相反数的一组是( )
A、-2与-
| |||
B、-2与
| |||
C、-2与
| |||
D、|-2|与
|
下列各数中,是无理数的为( )
A、
| |||
| B、3.14 | |||
C、
| |||
D、-
|
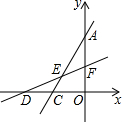 如图,A(0,4),C(-2,0),D(-4,0),过D点的直线交AC于E,交y轴于F,若S△DCE=S△AEF,求E点的坐标.
如图,A(0,4),C(-2,0),D(-4,0),过D点的直线交AC于E,交y轴于F,若S△DCE=S△AEF,求E点的坐标.