题目内容
15.已知$\sqrt{a(x-a)}$+$\sqrt{a(y-a)}$=$\sqrt{x-a}$-$\sqrt{a-y}$在实数范围内成立,其中a、x、y为互不相同的实数,求$\frac{x+y}{x-y}$的值.分析 根据二次根式有意义的条件得:被开方数为非负数,则a(x-a)≥0,x-a≥0,a(y-a)≥0,a-y≥0,所以a=0,先将a=0代入已知得:x=-y,最后再代入所求式子即可.
解答 解:∵a(x-a)≥0,x-a≥0,
∴a≥0,
∵a(y-a)≥0,a-y≥0,
∴a≤0,
∴a=0,
把a=0代入已知条件中得:$\sqrt{x}$-$\sqrt{-y}$=0,
x=-y,
则x+y=0,
∴$\frac{x+y}{x-y}$=0.
点评 本题考查了二次根式的化简求值:二次根式的化简求值,一定要先化简再代入求值.本题先根据二次根式有意义的条件得到字母的值或关系,然后代入所求的式子进行计算.

练习册系列答案
 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案
相关题目
10.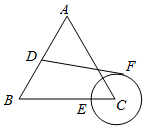 如图,等边△ABC的边长为4,D、E是边AB、BC上的动点(与A、B不重合),AD=2CE,以CE的长为半径作⊙C,DF与⊙C相切于F,下列关于DF的长说法正确的是( )
如图,等边△ABC的边长为4,D、E是边AB、BC上的动点(与A、B不重合),AD=2CE,以CE的长为半径作⊙C,DF与⊙C相切于F,下列关于DF的长说法正确的是( )
 如图,等边△ABC的边长为4,D、E是边AB、BC上的动点(与A、B不重合),AD=2CE,以CE的长为半径作⊙C,DF与⊙C相切于F,下列关于DF的长说法正确的是( )
如图,等边△ABC的边长为4,D、E是边AB、BC上的动点(与A、B不重合),AD=2CE,以CE的长为半径作⊙C,DF与⊙C相切于F,下列关于DF的长说法正确的是( )| A. | 有最大值,无最小值 | B. | 有最小值,无最大值 | ||
| C. | 有最大值,也有最小值 | D. | 为定值 |
20.已知A(-5,m2),B(-2,a),C(-0.5,b),D(4,c)都在反比例函数y=$\frac{k}{x}$的图象上,则下列判断正确的是( )
| A. | m2最大 | B. | a最大 | C. | b最大 | D. | c最大 |
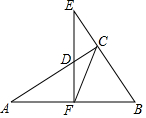 已知:如图,△ABC中,∠ACB=90°,F为AB的中点,EF⊥AB,求证:△CDF∽△ECF.
已知:如图,△ABC中,∠ACB=90°,F为AB的中点,EF⊥AB,求证:△CDF∽△ECF. 如图,已知四边形ABCD内接于⊙O,直径AC=6,对角线AC、BD交于E点,且AB=BD,EC=1,则AD的长是$\frac{3\sqrt{15}}{2}$.
如图,已知四边形ABCD内接于⊙O,直径AC=6,对角线AC、BD交于E点,且AB=BD,EC=1,则AD的长是$\frac{3\sqrt{15}}{2}$.