题目内容
13．
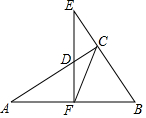已知：如图，△ABC中，∠ACB=90°，F为AB的中点，EF⊥AB，求证：△CDF∽△ECF．
分析 先根据直角三角形的性质得出AF=CF，∠A+∠B=90°，故可得出∠A=∠DCF，再由∠A+∠B=90°，∠B+∠E=90°可得出∠A=∠E，故∠E=∠DCF，由此可得出结论．
解答 证明：∵△ABC中，∠ACB=90°，F为AB的中点，
∴AF=CF，∠A+∠B=90°．
∴∠A=∠DCF．
∵EF⊥AB，
∴∠B+∠E=90°，
∴∠A=∠E，
∴∠E=∠DCF，
∴△CDF∽△ECF．
点评 本题考查的是相似三角形的判定，熟知相似三角形的判定定理是解答此题的关键．
练习册系列答案
相关题目
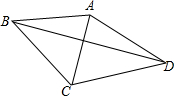如图，线段AB=a，将线段AB绕点A逆时针旋转60°得到线段AC，继续旋转α（0°＜α＜120°）得到线段AD，连接BC，CD，BD．
如图，在平面直角坐标系中，菱形OABC的顶点B在x轴上，其坐标为（6，0），菱形的面积为18$\sqrt{3}$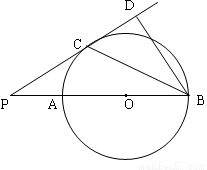
; 
.