题目内容
如图①,在平面直角坐标系中,A点坐标为(3,0),B点坐标为(0,4).动点M从点O出发,沿OA方向以每秒1个单位长度的速度向终点A运动;同时,动点N从点A出发沿AB方向以每秒
个单位长度的速度向终点B运动.设运动了x秒.
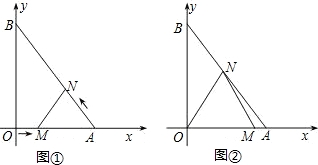
(1)点N的坐标为( , );(用含x的代数式表示)
(2)当x为何值时,△AMN为等腰三角形?
(3)如图②,连结ON得△OMN,△OMN可能为正三角形吗?若不能,点M的运动速度不变,试改变点N的运动速度,使△OMN为正三角形,并求出点N的运动速度和此时x的值.
| 5 |
| 3 |

(1)点N的坐标为(
(2)当x为何值时,△AMN为等腰三角形?
(3)如图②,连结ON得△OMN,△OMN可能为正三角形吗?若不能,点M的运动速度不变,试改变点N的运动速度,使△OMN为正三角形,并求出点N的运动速度和此时x的值.
考点:一次函数综合题
专题:
分析:(1)直接根据题意可表示出点N的坐标为(3-x,
x);
(2)注意要分3种情况考虑①AM=AN,②MN=AM,③MN=AN.用含x的代数式表示线段的长度,利用方程的思想求解即可;
(3)当N(
x,
x)时,△OMN为正三角形,由题意可得:NC∥BO,得出AN:NC=AB:BO,
=
,进而得出N点速度.
| 4 |
| 3 |
(2)注意要分3种情况考虑①AM=AN,②MN=AM,③MN=AN.用含x的代数式表示线段的长度,利用方程的思想求解即可;
(3)当N(
| 1 |
| 2 |
| ||
| 2 |
| AN | ||||
|
| 5 |
| 4 |
解答: 解:(1)如图,作NC⊥OA于x轴,
解:(1)如图,作NC⊥OA于x轴,
∵A点坐标为(3,0),B点坐标为(0,4),
∴OB=4,OA=3,
∴AB=
=5,
∵动点N从点A出发沿AB方向以每秒
个单位长度的速度向终点B运动,
∴AN=
x,
∵NC∥y轴,
∴
=
=
,
即:
=
=
,
解得:NC=
x,AC=x,
∴OC=3-x,
∴N(3-x,
x)
(2)①AM=AN,
x=3-x,
解得:x=
;
②MN=AM,
=3-x,
x(43x-54)=0,
x=0(舍去)或x=
,
③MN=AN,
x=
(3-x)
x=1
(3)不能,
 过点N作NC⊥OA,
过点N作NC⊥OA,
当N(
x,
x)时,△OMN为正三角形,
由题意可得:N的纵坐标为:
x,
∵NC∥BO,
∴AN:NC=AB:BO,
∴
=
,
解得:AN=
x,
N的速度即:
x÷x(N.M的时间都是x)=
,
此时x的值为
.
 解:(1)如图,作NC⊥OA于x轴,
解:(1)如图,作NC⊥OA于x轴,∵A点坐标为(3,0),B点坐标为(0,4),
∴OB=4,OA=3,
∴AB=
| 32+42 |
∵动点N从点A出发沿AB方向以每秒
| 5 |
| 3 |
∴AN=
| 5 |
| 3 |
∵NC∥y轴,
∴
| NC |
| OB |
| AC |
| AO |
| AN |
| AB |
即:
| NC |
| 4 |
| AC |
| 3 |
| ||
| 5 |
解得:NC=
| 4 |
| 3 |
∴OC=3-x,
∴N(3-x,
| 4 |
| 3 |
(2)①AM=AN,
| 5 |
| 3 |
解得:x=
| 9 |
| 8 |
②MN=AM,
(3-2x)2+(
|
x(43x-54)=0,
x=0(舍去)或x=
| 54 |
| 43 |
③MN=AN,
x=
| 1 |
| 2 |
x=1
(3)不能,
 过点N作NC⊥OA,
过点N作NC⊥OA,当N(
| 1 |
| 2 |
| ||
| 2 |
由题意可得:N的纵坐标为:
| ||
| 2 |
∵NC∥BO,
∴AN:NC=AB:BO,
∴
| AN | ||||
|
| 5 |
| 4 |
解得:AN=
5
| ||
| 8 |
N的速度即:
5
| ||
| 8 |
5
| ||
| 8 |
此时x的值为
5
| ||
| 8 |
点评:主要考查了函数和几何图形的综合运用.解题的关键是会灵活的运用函数图象的性质和交点的意义求出相应的线段的长度或表示线段的长度,再结合具体图形的性质求解.

练习册系列答案
相关题目

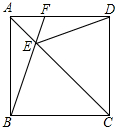 如图,在正方形ABCD中,AC为对角线,E为AC上一点,连接EB、ED.
如图,在正方形ABCD中,AC为对角线,E为AC上一点,连接EB、ED.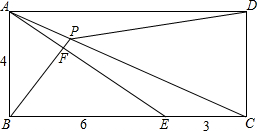 如图,在长方形ABCD中,AB=4,BE=6,EC=3,EF=2AF,BF的延长线交AC于P,则S△APD=
如图,在长方形ABCD中,AB=4,BE=6,EC=3,EF=2AF,BF的延长线交AC于P,则S△APD=