题目内容
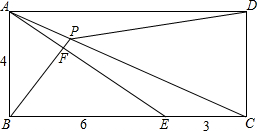 如图,在长方形ABCD中,AB=4,BE=6,EC=3,EF=2AF,BF的延长线交AC于P,则S△APD=
如图,在长方形ABCD中,AB=4,BE=6,EC=3,EF=2AF,BF的延长线交AC于P,则S△APD=考点:矩形的性质
专题:
分析:连接PE.易知S△ABE=12,S△AEC=6,由EF=2AF知S△ABF=4,S△BEF=8,设S△APF=x,则S△PEF=2x,S△PBE=2x+8,由BE=2EC知S△PEC=x+4,故x+2x+x+4=6?x=0.5.
=
=
=
=
=
,又由S△DAP+S△DPC=18,可求得S△DAP=4.5,S△DPC=13.5.
| S△EAP |
| S△EPC |
| 3x |
| x+4 |
| 1.5 |
| 4.5 |
| 1 |
| 3 |
| AP |
| PC |
| S△DAP |
| S△DPC |
解答: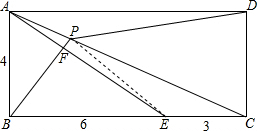 解:连接PE.
解:连接PE.
∵在长方形ABCD中,AB=4,BE=6,EC=3,
∴S△ABE=
AB•BE=12,S△AEC=
CE•AB=6,
∵EF=2AF,
∴S△ABF=
S△ABE=4,S△BEF=
S△ABE=8,
设S△APF=x,则S△PEF=2x,S△PBE=2x+8,
∵BE=2EC,
∴S△PEC=x+4,
∴x+2x+x+4=6,
解得:x=0.5.
∴
=
=
=
=
=
,
又∵S△DAP+S△DPC=18,
∴S△DAP=
×18=4.5,S△DPC=
×18=13.5.
故答案为:4.5.
 解:连接PE.
解:连接PE.∵在长方形ABCD中,AB=4,BE=6,EC=3,
∴S△ABE=
| 1 |
| 2 |
| 1 |
| 2 |
∵EF=2AF,
∴S△ABF=
| 1 |
| 3 |
| 2 |
| 3 |
设S△APF=x,则S△PEF=2x,S△PBE=2x+8,
∵BE=2EC,
∴S△PEC=x+4,
∴x+2x+x+4=6,
解得:x=0.5.
∴
| S△EAP |
| S△EPC |
| 3x |
| x+4 |
| 1.5 |
| 4.5 |
| 1 |
| 3 |
| AP |
| PC |
| S△DAP |
| S△DPC |
又∵S△DAP+S△DPC=18,
∴S△DAP=
| 1 |
| 4 |
| 3 |
| 4 |
故答案为:4.5.
点评:本题主要考查等积变换能力以及矩形的性质.此题难度适中,注意掌握辅助线的作法,注意掌握数形结合思想的应用.

练习册系列答案
 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案
相关题目
 A、B、C各点的位置如图.
A、B、C各点的位置如图.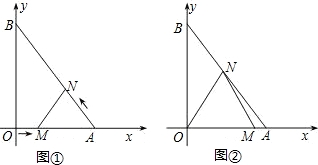
 如图,已知∠COB=2∠AOC,OD平分∠AOB,且∠COD=20°,则∠AOB的度数为
如图,已知∠COB=2∠AOC,OD平分∠AOB,且∠COD=20°,则∠AOB的度数为