题目内容
7．
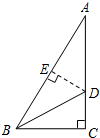如图，在Rt△ABC中，∠C=90°，∠ABC的平分线BD交AC于D，若CD=3cm，则点D到AB的距离DE是（ ）| A． | 2cm | B． | 3cm | C． | 4cm | D． | 5cm |
分析 根据角平分线上的点到角的两边距离相等可得DE=CD，再根据点到线段的距离的定义解答．
解答 解：过点D作DE⊥AB于E，
∵∠C=90°，BD是∠ABC的平分线，
∴DE=CD，
∵CD=3cm，
∴DE=3cm，
∴点D到AB的距离DE是3cm．
故选B．
点评 本题考查了角平分线上的点到角的两边距离相等的性质，点到线段的距离的定义，熟记性质与概念是解题的关键．
练习册系列答案
期末宝典单元检测分类复习卷系列答案
相关题目
17．
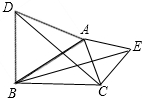已知：如图，△ABD和△ACE均为等腰三角形，且∠DAB=∠CAE=60°，则△ADC≌△AEB的根据是（ ）
已知：如图，△ABD和△ACE均为等腰三角形，且∠DAB=∠CAE=60°，则△ADC≌△AEB的根据是（ ）| A． | SSS | B． | SAS | C． | ASA | D． | AAS |
18．
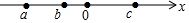实数a，b，c在数轴上对应的点如图，则下列式子中正确的是（ ）
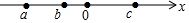实数a，b，c在数轴上对应的点如图，则下列式子中正确的是（ ）| A． | a-c＞b-c | B． | ac＞bc | C． | a+c＜b+c | D． | $\frac{a}{b}$＜$\frac{c}{b}$ |
15．一个数减去2等于-3，则这个数是（ ）
| A． | -5 | B． | -1 | C． | 1 | D． | 5 |
2．关于直线l：y=kx+k（k≠0），下列说法正确的是（ ）
| A． | l经过定点（1，0） | B． | l经过定点（-1，0） | ||
| C． | l经过第二、三、四象限 | D． | l经过第一、二、三象限 |
19．在平面直角坐标系中，抛物线y=-（x-1）2+2的顶点坐标是（ ）
| A． | （-1，2） | B． | （1，2） | C． | （2，-1） | D． | （2，1） |
如图，锐角△ABC是⊙O内接三角形，弦AE⊥BC，垂足为D．在AD上取点F，使FD=DE，连接CF，并延长交AB于点G．求证：CG⊥AB．
6．先阅读下列一段文字，然后解答问题：
某食品研究部门欲将甲、乙、丙三种食物混合研制成100千克食物，并规定：研制成的混合食品中至少需含44000单位的维生素A和48000单位的维生素B，三种食物的维生素A、B的含量如表1所示：
（表1）（表2）
设所取甲、乙、丙三种食物的质量分别为x千克、y千克、z千克，
（1）试根据题意列出等式和不等式，并说明：①y≥20；②2x-y≥40；
（2）设甲、乙、丙三种食物的生产成本如表2所示：①试用含x、y的代数式表示研制的混合食品的总成本P（元）；②如果限定混合食品中甲种食物的质量为40千克，试求此时总成本P的取值范围，并确定当P取最小值时，所取乙、丙两种食物的质量．
某食品研究部门欲将甲、乙、丙三种食物混合研制成100千克食物，并规定：研制成的混合食品中至少需含44000单位的维生素A和48000单位的维生素B，三种食物的维生素A、B的含量如表1所示：
| 甲种 食物 | 乙种 食物 | 丙种 食物 | 每千克生产成本（元） | |||
| 甲种食物 | 9 | |||||
| 维生素A（单位/千克） | 400 | 600 | 400 | 乙种食物 | 12 | |
| 维生素B（单位/千克） | 800 | 200 | 400 | 丙种食物 | 8 |
设所取甲、乙、丙三种食物的质量分别为x千克、y千克、z千克，
（1）试根据题意列出等式和不等式，并说明：①y≥20；②2x-y≥40；
（2）设甲、乙、丙三种食物的生产成本如表2所示：①试用含x、y的代数式表示研制的混合食品的总成本P（元）；②如果限定混合食品中甲种食物的质量为40千克，试求此时总成本P的取值范围，并确定当P取最小值时，所取乙、丙两种食物的质量．