题目内容
3. 如图,在△ABC中,AB=AC,∠BAC=50?.分别以B、C为圆心,BC长为半径画弧,设两弧交于点D,与AB、AC的延长线分别交于点E、F,连接AD.则
如图,在△ABC中,AB=AC,∠BAC=50?.分别以B、C为圆心,BC长为半径画弧,设两弧交于点D,与AB、AC的延长线分别交于点E、F,连接AD.则①∠DAE=25度;
②若BC=9,$\widehat{DE}$与$\widehat{DF}$的长度之和为$\frac{11}{2}$π.
分析 ①根据线段垂直平分线的判定和等腰三角形的性质即可得到结论;
②由等腰三角形的性质得出∠ABC=∠ACB=65°,由等边三角形的性质得出∠DBC=∠DCB=60°,再由平角的定义求出∠DBE=∠DCF=55°,然后根据弧长公式求出$\widehat{DE}$,$\widehat{DF}$的长度,即可得出结果.
解答  解:①连接CD,BD,
解:①连接CD,BD,
∵AB=AC,BD=CD,
∴AD垂直平分BC,
∴∠DAE=$\frac{1}{2}$∠BAC=25°;
故答案为:25;
②∵AB=AC,∠BAC=50,
∴∠ABC=∠ACB=65°,
∵BD=CD=BC,
∴△BDC为等边三角形,
∴∠DBC=∠DCB=60°,
∴∠DBE=∠DCF=55°,
∵BC=9,∴BD=CD=9,
∴$\widehat{DE}$的长度=$\widehat{DF}$的长度=$\frac{55π×9}{180}$=$\frac{11}{4}$π;
∴$\widehat{DE}$,$\widehat{DF}$的长度之和为$\frac{11}{2}$π.
故答案为:$\frac{11}{2}$π.
点评 本题考查了弧长的计算,等腰三角形的性质,等边三角形的判定与性质,平角的定义;熟练掌握等边三角形的判定与性质,并能进行推理计算是解决问题的关键.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
15.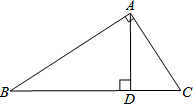 如图,在Rt△ABC中,∠BAC=90°,AD⊥BC于点D,则下列结论不正确的是( )
如图,在Rt△ABC中,∠BAC=90°,AD⊥BC于点D,则下列结论不正确的是( )
 如图,在Rt△ABC中,∠BAC=90°,AD⊥BC于点D,则下列结论不正确的是( )
如图,在Rt△ABC中,∠BAC=90°,AD⊥BC于点D,则下列结论不正确的是( )| A. | $sinB=\frac{AD}{AB}$ | B. | $sinB=\frac{AC}{BC}$ | C. | $sinB=\frac{AD}{AC}$ | D. | $sinB=\frac{CD}{AC}$ |

 如图,用扳手拧螺母时,旋转中心为螺丝(母)的中心,旋转角为0°~360°的任意角(答案不唯一).
如图,用扳手拧螺母时,旋转中心为螺丝(母)的中心,旋转角为0°~360°的任意角(答案不唯一). 如图,△ABC是边长为1的正三角形,弧AB和弧AC所对的圆心角均为120°,则图中阴影部分的面积为$\frac{\sqrt{3}}{12}$.
如图,△ABC是边长为1的正三角形,弧AB和弧AC所对的圆心角均为120°,则图中阴影部分的面积为$\frac{\sqrt{3}}{12}$.