题目内容
6.因式分解:x2-2xy-3y2+3x-5y+2.分析 先分解x2-2xy-3y2=(x-3y)(x+y),那么原式=(x-3y+A)(x+y+B)=x2-2xy-3y2+Ax+Ay+Bx-3By+AB,则:$\left\{\begin{array}{l}{A+B=3}\\{A-3B=5}\end{array}\right.$,解得:$\left\{\begin{array}{l}{A=1}\\{B=2}\end{array}\right.$,即可解答.
解答 解:x2-2xy-3y2=(x-3y)(x+y),
那么原式=(x-3y+A)(x+y+B)=x2-2xy-3y2+Ax+Ay+Bx-3By+AB,
则:$\left\{\begin{array}{l}{A+B=3}\\{A-3B=5}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{A=1}\\{B=2}\end{array}\right.$
原式=(x-3y+1)(x+y+2).
点评 本题考查了分组分解法,解决本题的关键是先利用待定系数法进行分解因式.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
16.若a是有理数,则整式a(a-2)-2a+5的值为( )
| A. | 不是负数 | B. | 恒为正数 | C. | 恒为负数 | D. | 不等于零 |
 如图,在菱形ABCD中,E是AB的中点,且DE⊥AB,AB=4,求:
如图,在菱形ABCD中,E是AB的中点,且DE⊥AB,AB=4,求: 如图△ABC,用直尺和圆规按要求作图(不写作法,保留作图痕迹)
如图△ABC,用直尺和圆规按要求作图(不写作法,保留作图痕迹)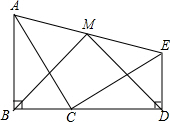 如图,△ABC≌△CDE,B、C、D三点共线,连接AE,点M为AE中点,连接BM、DM,试判断△BMD的形状.
如图,△ABC≌△CDE,B、C、D三点共线,连接AE,点M为AE中点,连接BM、DM,试判断△BMD的形状.