题目内容
①用甲图所示的大小正方形和长方形卡片若干张,拼成一个长为2a+b,宽为a+b的矩形,需要A类卡片 张,B类卡片 张,C类卡片 张.
②现有长为a+3b,宽为a+b的长方形(如乙图),你能用上属三类卡片拼出这个长方形吗?试试看!
②现有长为a+3b,宽为a+b的长方形(如乙图),你能用上属三类卡片拼出这个长方形吗?试试看!

考点:多项式乘多项式
专题:计算题
分析:①利用多项式乘以多项式法则计算(2a+b)(a+b),得到结果,即可做出判断;
②利用多项式乘以多项式法则计算(a+3b)(a+b),得到结果,即可做出判断.
②利用多项式乘以多项式法则计算(a+3b)(a+b),得到结果,即可做出判断.
解答:解:① 长为2a+b,宽为a+b的矩形面积为(2a+b)(a+b)=2a2+3ab+b2,
长为2a+b,宽为a+b的矩形面积为(2a+b)(a+b)=2a2+3ab+b2,
A图形面积为a2,B图形面积为ab,C图形面积为b2,
则可知需要A类卡片2张,B类卡片3张,C类卡片1张.
故本题答案为:2;3;1;
②∵现有长为a+3b,宽为a+b的长方形,
∴(a+3b)(a+b)=a2+4ab+3b2,
∵A图形面积为a2,B图形面积为ab,C图形面积为b2,
∴可知需要A类卡片1张,B类卡片4张,C类卡片3张;
(2a+b)(a+b)=2a2+3ab+b2,
则拼成一个长为2a+b,宽为a+b的矩形,需要A类卡片2张,B类卡片3张,C类卡片1张.
 长为2a+b,宽为a+b的矩形面积为(2a+b)(a+b)=2a2+3ab+b2,
长为2a+b,宽为a+b的矩形面积为(2a+b)(a+b)=2a2+3ab+b2,A图形面积为a2,B图形面积为ab,C图形面积为b2,
则可知需要A类卡片2张,B类卡片3张,C类卡片1张.
故本题答案为:2;3;1;
②∵现有长为a+3b,宽为a+b的长方形,
∴(a+3b)(a+b)=a2+4ab+3b2,
∵A图形面积为a2,B图形面积为ab,C图形面积为b2,
∴可知需要A类卡片1张,B类卡片4张,C类卡片3张;
(2a+b)(a+b)=2a2+3ab+b2,
则拼成一个长为2a+b,宽为a+b的矩形,需要A类卡片2张,B类卡片3张,C类卡片1张.
点评:此题考查了多项式乘多项式,熟练掌握运算法则是解本题的关键.

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目
 如图,AD=BC,AC=BD,则下列结论中,不正确的是( )
如图,AD=BC,AC=BD,则下列结论中,不正确的是( )| A、OA=OB |
| B、∠AOB=∠C+∠D |
| C、CO=DO |
| D、∠C=∠D |
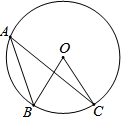 如图,点A、B、C在⊙O上,∠B=52°,∠C=18°,则∠A的度数为( )
如图,点A、B、C在⊙O上,∠B=52°,∠C=18°,则∠A的度数为( )| A、30° | B、20° |
| C、34° | D、28° |
 如图,OA是⊙O的半径,弦BC⊥OA,D是⊙O上一点,若∠ADB=28°,则∠AOC的度数为( )
如图,OA是⊙O的半径,弦BC⊥OA,D是⊙O上一点,若∠ADB=28°,则∠AOC的度数为( )| A、14° | B、28° |
| C、56° | D、84° |
 如图,已知E是等腰梯形ABCD的腰BC的中点,AE把梯形分成四边形AECD和△AEB,且四边形AECD的周长比△AEB周长要多4cm,若AB=12cm,CD=2cm,求梯形的腰AD长.
如图,已知E是等腰梯形ABCD的腰BC的中点,AE把梯形分成四边形AECD和△AEB,且四边形AECD的周长比△AEB周长要多4cm,若AB=12cm,CD=2cm,求梯形的腰AD长.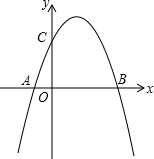 如图,抛物线y=ax2-3ax+b与x轴交于A和B(4,0),与y轴交于C点,并且OB=OC,点P为抛物线上一点.
如图,抛物线y=ax2-3ax+b与x轴交于A和B(4,0),与y轴交于C点,并且OB=OC,点P为抛物线上一点.