题目内容
1.为了迎接全运会在济南的召开,山东综艺频道举办了“全运向前冲”节目.为方便观众观看节目,闯关场地的外围围墙用若干块长为5米,宽为2.5米的长方形帆布缝制而成,两块帆布缝合的公共部分是0.1米,围成的围墙高2.5米.(1)若先用6块帆布缝制成宽为2.5米的条形,求其长度.
(2)若使围成的圆形场地的半径为$\frac{147}{π}$米,则需要买几块这样的帆布缝制围墙?
分析 (1)用帆布的长度减去公共部分即可;
(2)根据帆布的总长度-公共部分=圆的周长求解即可.
解答 解:(1)6×5-5×0.1=29.5(米).
答:其长度为29.5米.
(2)设至少需要买x块这样的帆布缝制围墙.
根据题意得:5x-0.1x=2π×$\frac{147}{π}$,
解得:x=60.
答:需要买60块这样的帆布缝制围墙.
点评 本题主要考查的是元一次方程的应用,根据帆布的总长度-公共部分=圆的周长列出关于x的方程是解题的关键.

练习册系列答案
相关题目
9.若式子$\frac{3x-2}{2}$与$\frac{2x+1}{3}$的值相等,则x的值是( )
| A. | 1 | B. | $\frac{8}{5}$ | C. | $\frac{5}{8}$ | D. | 2 |
16.方程ax+1=3的解是x=-2,则a的值是( )
| A. | 2 | B. | 1 | C. | -1 | D. | -2 |
 如图,在△ABC中,D是BC上一点,∠1=∠2,∠BAC=68°,∠3=70°,求∠4的度数.
如图,在△ABC中,D是BC上一点,∠1=∠2,∠BAC=68°,∠3=70°,求∠4的度数.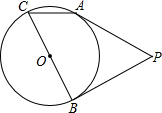 如图,PA,PB切⊙O于点A,B,BC是⊙O的直径,∠C=55°,则∠P=50°.
如图,PA,PB切⊙O于点A,B,BC是⊙O的直径,∠C=55°,则∠P=50°. 如图9个方格中,每行、每列、每条对角线上的三个数的和都相等.那么,右上角的数为2011.
如图9个方格中,每行、每列、每条对角线上的三个数的和都相等.那么,右上角的数为2011. 如图,在△ABC中,AD⊥BC于D,M、N分别是AB、AC的中点,连接DM、DN.
如图,在△ABC中,AD⊥BC于D,M、N分别是AB、AC的中点,连接DM、DN.