题目内容
6.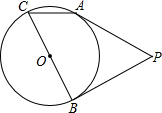 如图,PA,PB切⊙O于点A,B,BC是⊙O的直径,∠C=55°,则∠P=50°.
如图,PA,PB切⊙O于点A,B,BC是⊙O的直径,∠C=55°,则∠P=50°.
分析 连接OB,首先根据等腰三角形的性质及三角形内角和定理,求出∠BOA的度数;由于∠OAP和∠OBP都是直角,由四边形的内角和为360°可知:∠AOB和∠P互补,由此可求出∠P的度数.
解答 解:连接OB.
∵PA、PB都是⊙O的切线,且切点为A、B,
∴∠OAP=∠OBP=90°.
∴∠AOB+∠P=180°.
∵∠C=65°,
∴∠AOB=130°.
∴∠P=180°-130°=50°.
点评 此题主要考查的是切线的性质、等腰三角形的性质以及三角形内角和定理,求得∠AOB+∠P=180°是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
15.已知反比例函数y=-$\frac{2}{x}$的图象上有两点A(x1,y1),B(x2,y2),且x1<x2<0,则y1,y2的大小关系为( )
| A. | y1<y2 | B. | y1>y2 | C. | y1=y2 | D. | 无法确定 |
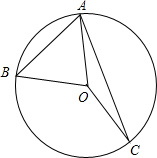 如图,已知点A、B、C在⊙0上,且$\widehat{AB}:\widehat{BC}:\widehat{AC}$=2:3:4.
如图,已知点A、B、C在⊙0上,且$\widehat{AB}:\widehat{BC}:\widehat{AC}$=2:3:4.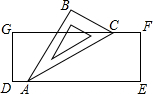 如图,小聪把一块含有30°角的直角三角尺ABC的两个顶点A,C放在长方形纸片DEFG的对边上,若AC平分∠BAE,则∠DAB的度数是120°.
如图,小聪把一块含有30°角的直角三角尺ABC的两个顶点A,C放在长方形纸片DEFG的对边上,若AC平分∠BAE,则∠DAB的度数是120°. 如图,两个圆是以点O为圆心的同心圆,大圆的弦AB是小圆的切线,C为切点,C是AB的中点吗?为什么?
如图,两个圆是以点O为圆心的同心圆,大圆的弦AB是小圆的切线,C为切点,C是AB的中点吗?为什么?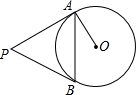 如图,PA、PB分别切⊙0于A、B两点,求证:∠APB=2∠BAO.
如图,PA、PB分别切⊙0于A、B两点,求证:∠APB=2∠BAO.