题目内容
16. 如图,一汽车在坡角为30°的斜坡点A开始爬行,行驶了150米到达点B,则这时汽车在水平方向前进的距离AC为75$\sqrt{3}$米.
如图,一汽车在坡角为30°的斜坡点A开始爬行,行驶了150米到达点B,则这时汽车在水平方向前进的距离AC为75$\sqrt{3}$米.
分析 连结BC,则∠ACB=90°.在Rt△ABC中,根据锐角三角函数的定义可得出AC=AB•cos∠BAC,再由特殊角的三角函数值解答即可.
解答  解:连结BC,则∠ACB=90°.
解:连结BC,则∠ACB=90°.
∵在Rt△ABC中,∵∠ACB=90°,AB=150米,∠BAC=30°,
∴cos∠BAC=$\frac{AC}{AB}$,
∴AC=AB•cos∠BAC=150×$\frac{\sqrt{3}}{2}$=75$\sqrt{3}$(米).
故答案为:75$\sqrt{3}$.
点评 本题考查的是解直角三角形的应用-坡度坡角问题,熟知锐角三角函数的定义及特殊角的三角函数值是解答此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
6.下列多项式能用完全平方公式分解因式的是( )
| A. | x2-1 | B. | x2-2x+4 | C. | x2+2x+1 | D. | x2+x |
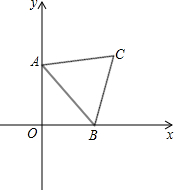 如图,直线y=-$\frac{3}{4}$x+6与坐标轴分别相交于点A、B.
如图,直线y=-$\frac{3}{4}$x+6与坐标轴分别相交于点A、B. 如图,已知AE∥BC,∠B=50°,AE平分∠DAC,则∠DAC=100°.
如图,已知AE∥BC,∠B=50°,AE平分∠DAC,则∠DAC=100°.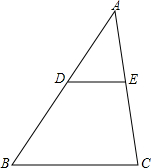 如图,△ABC中,∠ADE=∠B=60°,∠AED=70°,则∠C=70°.
如图,△ABC中,∠ADE=∠B=60°,∠AED=70°,则∠C=70°.