题目内容
5.平面内的两条直线有相交和平行两种位置关系.(1)如图1,若AB∥CD,点P在AB,CD内部,则∠BPD,∠B,∠D之间有何数量关系?请说明你的结论.
(2)在图1中,将直线AB绕点B逆时针方向旋转一定角度交直线CD于点Q,如图2,则∠BPD,∠B,∠D,∠BQD之间的关系为∠B+∠D+∠BQD=∠BPD;
(3)根据(2)的结论求图3中∠A+∠B+∠C+∠D+∠E+∠F+∠G的度数.

分析 (1)过P作PE∥AB,根据平行线的性质可求得∠BPD=∠B+∠D;
(2)过B作BF∥CD,结合(1)的结论和平行线的性质可得到∠BPD=∠ABP+∠D+∠BQD;
(3)根据三角形内角与外角的关系可得∠A+∠F=∠1,∠B+∠G=∠2,进而可得∠A+∠F+∠B+∠G=∠1+∠2,再根据多边形内角和可得答案.
解答 解:(1)∠BPD=∠B+∠D;
过P作PE∥AB,
∵AB∥CD,
∴PE∥AB∥CD,
∴∠1=∠ABP,∠2=∠CDP,
∴∠BPD=∠B+∠D;
(2)延长BP交CD于E,
∵∠B+∠BQD=∠BED,∠D+∠BED=∠BPD,
∴∠B+∠D+∠BQD=∠BPD;
故答案为:∠B+∠D+∠BQD=∠BPD.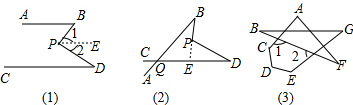
(3)∵∠A+∠F=∠1,∠B+∠G=∠2,
∴∠A+∠F+∠B+∠G=∠1+∠2,
∵∠1+∠2+∠C+∠D+∠E=540°,
∴∠A+∠F+∠B+∠G+∠C+∠D+∠E=540°.
点评 本题主要考查平行线的性质,三角形形内角与外角的关系,关键是掌握三角形的外角等于与它不相邻的两个内角的和.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
14.下列说法中,正确的是( )
| A. | 2不是单项式 | B. | -ab2的系数是-1,次数是3 | ||
| C. | 6πx3的系数是6 | D. | -$\frac{{2{x^2}y}}{3}$的系数是-2 |
15.$\sqrt{43}$介于哪两个整数之间( )
| A. | 4与5 | B. | 5与6 | C. | 6与7 | D. | 7与8 |
 如图,点A,B在数轴上,它们所对应的数分别是-3和$\frac{1-x}{2-x}$,且点A,B到原点的距离相等,则x=2.5.
如图,点A,B在数轴上,它们所对应的数分别是-3和$\frac{1-x}{2-x}$,且点A,B到原点的距离相等,则x=2.5. 如图,一汽车在坡角为30°的斜坡点A开始爬行,行驶了150米到达点B,则这时汽车在水平方向前进的距离AC为75$\sqrt{3}$米.
如图,一汽车在坡角为30°的斜坡点A开始爬行,行驶了150米到达点B,则这时汽车在水平方向前进的距离AC为75$\sqrt{3}$米.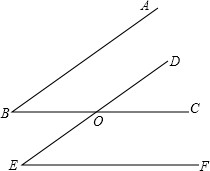 如图,已知:BC交DE于O,给出下面三个论断:①∠B=∠E;②AB∥DE;③BC∥EF.请以其中的两个论断为条件,填入“题设”栏中,以一个论断为结论,填入“结论”栏中,使之成为一个正确的命题,并加以证明.
如图,已知:BC交DE于O,给出下面三个论断:①∠B=∠E;②AB∥DE;③BC∥EF.请以其中的两个论断为条件,填入“题设”栏中,以一个论断为结论,填入“结论”栏中,使之成为一个正确的命题,并加以证明.