题目内容
1．已知$\root{3}{x}$=4，且（y-2x+1）2+$\sqrt{z-3}$=0，求$\root{3}{（x+y）^{3}+{z}^{3}}$的值．分析 根据立方根与非负数的性质得出x=64，z=3，y=127，再代入解答即可．
解答 解：根据题意可得：x=64，y-2x+1=0，z-3=0，
解得：x=64，z=3，y=127，
把x=64，z=3，y=127代入$\root{3}{（x+y）^{3}+{z}^{3}}$=$\root{3}{（127+64）^{3}+{3}^{3}}$=$2\root{3}{870985}$．
点评 本题考查了立方根，关键是根据如果一个数的立方等于a，那么这个数叫做a的立方根或三次方根．
练习册系列答案
相关题目
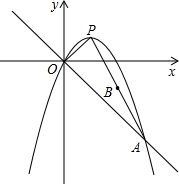如图，已知直线y=-x与二次函数y=-x2+bx+c的图象交于点A、O，O是坐标原点，OA=3$\sqrt{2}$，点P为二次函数图象的顶点，点B是AP的中点．