题目内容
18.已知:a、b是常数,若关于m、n的二元一次方程组$\left\{\begin{array}{l}{am+bn=9.1}\\{3am+2bn=6.7}\end{array}\right.$的解是$\left\{\begin{array}{l}{m=3.1}\\{n=1.7}\end{array}\right.$,则关于x、y的二元一次方程组$\left\{\begin{array}{l}{a(x+1)+b(y-2)=9.1}\\{3a(x+1)+2b(y-2)=6.7}\end{array}\right.$的解是$\left\{\begin{array}{l}{x=2.1}\\{y=3.7}\end{array}\right.$.分析 把$\left\{\begin{array}{l}{m=3.1}\\{n=1.7}\end{array}\right.$代入二元一次方程组$\left\{\begin{array}{l}{am+bn=9.1}\\{3am+2bn=6.7}\end{array}\right.$,得出a和b的值后代入二元一次方程组$\left\{\begin{array}{l}{a(x+1)+b(y-2)=9.1}\\{3a(x+1)+2b(y-2)=6.7}\end{array}\right.$解答即可.
解答 解:把$\left\{\begin{array}{l}{m=3.1}\\{n=1.7}\end{array}\right.$代入二元一次方程组$\left\{\begin{array}{l}{am+bn=9.1}\\{3am+2bn=6.7}\end{array}\right.$,
可得:$\left\{\begin{array}{l}{3.1a+1.7b=9.1}\\{9.3a+3.4b=6.7}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{a=\frac{115}{31}}\\{b=\frac{206}{17}}\end{array}\right.$,
把a和b的值代入二元一次方程组$\left\{\begin{array}{l}{a(x+1)+b(y-2)=9.1}\\{3a(x+1)+2b(y-2)=6.7}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{x=2.1}\\{y=3.7}\end{array}\right.$.
点评 此题考查了二元一次方程组的解,方程组的解即为能使方程组中两方程成立的未知数的值.

 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案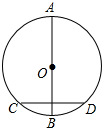 如图,AB为⊙O的直径,CD⊥AB,若AB=10,CD=8,则圆心O到弦CD的距离为( )
如图,AB为⊙O的直径,CD⊥AB,若AB=10,CD=8,则圆心O到弦CD的距离为( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
| A. | 平行四边形的对角相等 | B. | 正方形的对角线相等 | ||
| C. | 对角线相等的平行四边形是矩形 | D. | 对角线互相垂直的四边形是菱形 |
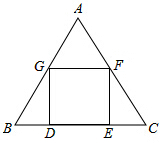 △ABC是一块等边三角形的废铁片,利用其剪裁一个正方形DEFG,使正方形的一条边DE落在BC上,顶点F、G分别落在AC、AB上.
△ABC是一块等边三角形的废铁片,利用其剪裁一个正方形DEFG,使正方形的一条边DE落在BC上,顶点F、G分别落在AC、AB上.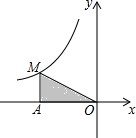 如图,M为反比例函数y=$\frac{k}{x}$(x<0)的图象上一点,MA⊥x轴,垂足为点A,△AMO的面积为3,则k的值为-6.
如图,M为反比例函数y=$\frac{k}{x}$(x<0)的图象上一点,MA⊥x轴,垂足为点A,△AMO的面积为3,则k的值为-6.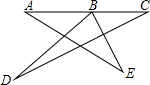 如图所示,试求∠A+∠DBE+∠C+∠D+∠E=180°.
如图所示,试求∠A+∠DBE+∠C+∠D+∠E=180°.