题目内容
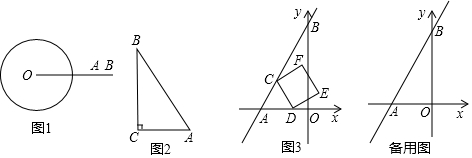
14. 菱形OBCD在平面直角坐标系中的位置如图所示,顶点B(2,0),∠DOB=60°,点E坐标为(0,-$\sqrt{3}$),点P是对角线OC上一个动点,则EP+BP最短的最短距离为$\sqrt{13}$.
菱形OBCD在平面直角坐标系中的位置如图所示,顶点B(2,0),∠DOB=60°,点E坐标为(0,-$\sqrt{3}$),点P是对角线OC上一个动点,则EP+BP最短的最短距离为$\sqrt{13}$.
分析 点B的对称点是点D,连接ED,交OC于点P,再得出ED即为EP+BP最短,解答即可.
解答 解:连接ED,如图,
∵点B的对称点是点D,
∴DP=BP,
∴ED即为EP+BP最短,
∵四边形ABCD是菱形,顶点B(2,0),∠DOB=60°,
∴点D的坐标为(1,$\sqrt{3}$),
∵点E的坐标为(0,-$\sqrt{3}$),
直线ED=$\sqrt{{1}^{2}+(2\sqrt{3})^{2}}$=$\sqrt{13}$,
故答案为:$\sqrt{13}$.
点评 此题考查菱形的性质,关键是根据一次函数与方程组的关系,得出两直线的解析式,求出其交点坐标.

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目
5.若a与-5互为相反数,则a的值是( )
| A. | $-\frac{1}{5}$ | B. | $\frac{1}{5}$ | C. | -5 | D. | 5 |
9.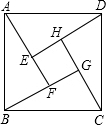 如图是我国汉代数学家赵爽在注解《周脾算经》时给出的“赵爽弦图”,图中的四个直角三角形是全等的,如果大正方形ABCD的面积是小正方形EFGH面积的13倍,那么tan∠ADE的值为( )
如图是我国汉代数学家赵爽在注解《周脾算经》时给出的“赵爽弦图”,图中的四个直角三角形是全等的,如果大正方形ABCD的面积是小正方形EFGH面积的13倍,那么tan∠ADE的值为( )
 如图是我国汉代数学家赵爽在注解《周脾算经》时给出的“赵爽弦图”,图中的四个直角三角形是全等的,如果大正方形ABCD的面积是小正方形EFGH面积的13倍,那么tan∠ADE的值为( )
如图是我国汉代数学家赵爽在注解《周脾算经》时给出的“赵爽弦图”,图中的四个直角三角形是全等的,如果大正方形ABCD的面积是小正方形EFGH面积的13倍,那么tan∠ADE的值为( )| A. | $\frac{3}{2}$ | B. | $\frac{1}{2}$ | C. | $\frac{2}{3}$ | D. | $\frac{{2\sqrt{13}}}{13}$ |
19. 数轴上有A,B,C,D四个点,其中表示互为相反数的两个点是( )
数轴上有A,B,C,D四个点,其中表示互为相反数的两个点是( )
 数轴上有A,B,C,D四个点,其中表示互为相反数的两个点是( )
数轴上有A,B,C,D四个点,其中表示互为相反数的两个点是( )| A. | 点B与点C | B. | 点A与点C | C. | 点A与点D | D. | 点B与点D |
6.用配方法解一元二次方程x2-4x=5时,下列配方正确的是( )
| A. | (x-2)2=9 | B. | (x-2)2=1 | C. | (x+2)2=9 | D. | (x+2)2=1 |
3.-$\frac{1}{3}$的倒数是( )
| A. | $\frac{1}{3}$ | B. | -$\frac{1}{3}$ | C. | 3 | D. | -3 |
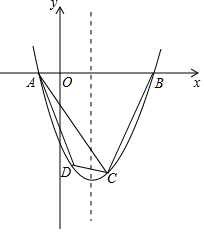 如图,在平面直角坐标系中,已知抛物线y=x2+bx+c经过A、B、C三点,已知B(4,0),C(2,-6).
如图,在平面直角坐标系中,已知抛物线y=x2+bx+c经过A、B、C三点,已知B(4,0),C(2,-6).