题目内容
3．下列说法中，正确的有（ ）（1）$\sqrt{25}$的平方根是±5；
（2）五边形的内角和是540°．
（3）抛物线y=x2+2x+4与x轴无交点．
（4）等腰三角形两边长为6cm和4cm，则它的周长是16cm．
| A． | 2个 | B． | 3个 | C． | 4个 | D． | 5个 |
分析 根据抛物线与x轴交点、平方根、三角形三边关系以及等腰三角形的性质等知识判断各个选项即可．
解答 解：（1）$\sqrt{25}$的平方根是±$\sqrt{5}$，错误；
（2）五边形的内角和是540°，正确；
（3）抛物线y=x2+2x+4与x轴无交点，△=4-16=-12＜0，正确；
（4）等腰三角形两边长为6cm和4cm，则它的周长是16cm或14cm，错误；
正确的有（2）（3），
故选A．
点评 本题主要考查了抛物线与x轴交点、平方根、三角形三边关系以及等腰三角形的性质等知识，解答本题的关键是熟练掌握各个知识点的定义以及性质，此题难度不大．
练习册系列答案
期末好成绩系列答案
99加1领先期末特训卷系列答案
百强名校期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案
金状元绩优好卷系列答案
相关题目
13．
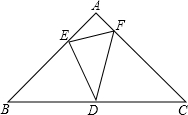△ABC是等腰直角三角形，∠A=90°，AB=$\sqrt{2}$，点D位于边BC的中点上．点E在AB上，点F在AC上，∠EDF=45°，给出以下结论：
①当BE=1时，S△CDF=$\frac{\sqrt{2}}{2}$；②∠DFC=∠EDB；③CF•BE=1；④C△AEF=$\sqrt{2}$；⑤S△AEF+2S△DEF=$\frac{1}{2}$；
正确的有（ ）
△ABC是等腰直角三角形，∠A=90°，AB=$\sqrt{2}$，点D位于边BC的中点上．点E在AB上，点F在AC上，∠EDF=45°，给出以下结论：①当BE=1时，S△CDF=$\frac{\sqrt{2}}{2}$；②∠DFC=∠EDB；③CF•BE=1；④C△AEF=$\sqrt{2}$；⑤S△AEF+2S△DEF=$\frac{1}{2}$；
正确的有（ ）
| A． | ①②③ | B． | ①③④⑤ | C． | ②③④ | D． | ③④⑤ |
11．抛物线y=ax2+bx+3（a≠0）过A（4，4），B（2，m）两点，点B到抛物线对称轴的距离记为d，满足0＜d≤1，则实数m的取值范围是（ ）
| A． | m≤2或m≥3 | B． | m≤3或m≥4 | C． | 2＜m＜3 | D． | 3＜m＜4 |
如图，在等腰△ABC中，AB=AC，两底角的平分线BE和CD相交于O点，求证：BE=CD．
8．根据下列表格中的数值，判断方程ax2+bx+c=0（a，b为常数）根的情况（ ）
| x | … | -1 | 0 | 1 | 2 | 3 | … |
| ax2+bx+c | … | -3 | 2 | 3 | 0 | -7 | … |
| A． | 有两个不相等实根 | B． | 有两个相等实根 | ||
| C． | 只有一个实根 | D． | 无实根 |
12．
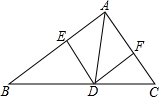如图，在△ABC中，DE∥CA，DF∥BA，下列四个判断不正确的是（ ）
如图，在△ABC中，DE∥CA，DF∥BA，下列四个判断不正确的是（ ）| A． | 四边形AEDF是平行四边形 | |
| B． | 如果∠BAC=90°，那么四边形AEDF是矩形 | |
| C． | 如果AD平分∠BAC，那么四边形AEDF是矩形 | |
| D． | 如果AD⊥BC，且AB=AC，那么四边形AEDF是菱形 |
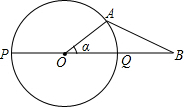如图，PQ为⊙O的直径，点B在线段PQ的延长线上，OQ=QB=1，动点A在⊙O的上半圆运动（含P、Q两点），连结AB，设∠AOB=α．有以下结论：