题目内容
14.一个袋子中只装有黑、白两种颜色的球,这些球的形状、质地等完全相同,其中白色球有2个,黑色球有n个.在看不到球的条件下,随机地从袋子中摸出一个球,记录下颜色后,放回袋子中并摇匀.同学们进行了大量重复试验,发现摸出白球的频率稳定在0.4附近,则n的值为( )| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
分析 根据白球的频率稳定在0.4附近得到白球的概率约为0.4,根据白球个数确定出总个数,进而确定出黑球个数.
解答 解:根据题意得:$\frac{2}{2+n}$=0.4,
解得:n=3,
则n的值为3,
故选B.
点评 此题考查了利用频率估计概率,解答此题的关键是了解白球的频率稳定在0.4附近即为概率约为0.4.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
19.等腰△ABC的周长为10,则其腰长x的取值范围是( )
| A. | x>$\frac{5}{2}$ | B. | x<5 | C. | $\frac{5}{2}$<x<5 | D. | $\frac{5}{2}$≤x≤5 |
6.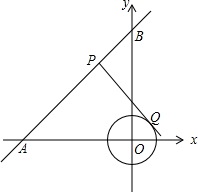 如图,在平面直角坐标系中,⊙O的半径为1,点P在经过点A(-3,0)、B(0,4)的直线上,PQ切⊙O于点Q,则切线长PQ的最小值为( )
如图,在平面直角坐标系中,⊙O的半径为1,点P在经过点A(-3,0)、B(0,4)的直线上,PQ切⊙O于点Q,则切线长PQ的最小值为( )
 如图,在平面直角坐标系中,⊙O的半径为1,点P在经过点A(-3,0)、B(0,4)的直线上,PQ切⊙O于点Q,则切线长PQ的最小值为( )
如图,在平面直角坐标系中,⊙O的半径为1,点P在经过点A(-3,0)、B(0,4)的直线上,PQ切⊙O于点Q,则切线长PQ的最小值为( )| A. | $\sqrt{7}$ | B. | $\frac{\sqrt{119}}{5}$ | C. | 2.4 | D. | 3 |
 如图,DE为△ABC的中位线,点F在DE上,且∠AFB=90°,若EF=2,BC=10,则AB的长为6.
如图,DE为△ABC的中位线,点F在DE上,且∠AFB=90°,若EF=2,BC=10,则AB的长为6.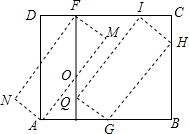 如图所示,将矩形ABCD纸板剪出一个宽AE=5的矩形AEFD,再将它绕着中心O顺时针旋转,使其中两个顶点分别与点A和点F重合,得到矩形AMFN,再沿着直线AB向右平移使点M和点N分别落在边BC和边EF上,得到矩形GHIJ,当$\frac{AD}{AB}$=$\frac{5}{6}$时,矩形ABCD的周长为66.
如图所示,将矩形ABCD纸板剪出一个宽AE=5的矩形AEFD,再将它绕着中心O顺时针旋转,使其中两个顶点分别与点A和点F重合,得到矩形AMFN,再沿着直线AB向右平移使点M和点N分别落在边BC和边EF上,得到矩形GHIJ,当$\frac{AD}{AB}$=$\frac{5}{6}$时,矩形ABCD的周长为66.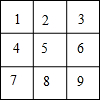 如图,九个小朋友用抽签的方式来确定各自的座位(如图中1~9这9个座位),小明第一个抽,抽到6号座位,小华第二个抽,那么小华抽到的座位恰好和小明的座位相邻的概率是$\frac{3}{8}$.
如图,九个小朋友用抽签的方式来确定各自的座位(如图中1~9这9个座位),小明第一个抽,抽到6号座位,小华第二个抽,那么小华抽到的座位恰好和小明的座位相邻的概率是$\frac{3}{8}$.