题目内容
4. 如图,DE为△ABC的中位线,点F在DE上,且∠AFB=90°,若EF=2,BC=10,则AB的长为6.
如图,DE为△ABC的中位线,点F在DE上,且∠AFB=90°,若EF=2,BC=10,则AB的长为6.
分析 延长AF交BC于M,首先证明AF=FM,再证明BA=BM,CM=2EF即可解决问题.
解答 解:延长AF交BC于M.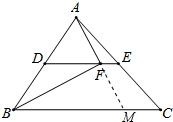
∵DE为△ABC的中位线,
∴AD=BD,AE=EC,DE∥BC,
∴AF=FM,
∵BF⊥AM,
∴BA=BM,
∵AF=FM,AE=EC,
∴CM=2EF=4,
∴BM=BC-CM=6,
∴AB=BM=6.
故答案为6.
点评 本题考查三角形中位线定理、解题的关键是出现中点想到三角形中位线定理,记住三角形中位线平行于第三边且等于第三边的一半,学会添加常用辅助线,属于中考常考题型.

练习册系列答案
相关题目
6. 如图,AB∥CD,DA⊥AC,垂足为A,若∠ADC=35°,则∠1的度数为( )
如图,AB∥CD,DA⊥AC,垂足为A,若∠ADC=35°,则∠1的度数为( )
 如图,AB∥CD,DA⊥AC,垂足为A,若∠ADC=35°,则∠1的度数为( )
如图,AB∥CD,DA⊥AC,垂足为A,若∠ADC=35°,则∠1的度数为( )| A. | 65° | B. | 55° | C. | 45° | D. | 35° |
7.已知一组数据75,80,80,85,90,则它的众数和中位数分别为( )
| A. | 75,80 | B. | 80,85 | C. | 80,90 | D. | 80,80 |
12.已知∠1=37°36′,∠2=37.36°,则∠1与∠2的大小关系为( )
| A. | ∠1<∠2 | B. | ∠1=∠2 | C. | ∠1>∠2 | D. | 无法比较 |
13.一个等腰三角形的两条边长分别3和6,则该等腰三角形的周长是( )
| A. | 12 | B. | 13 | C. | 15 | D. | 12或15 |
 如图,AB是⊙O直径,CD⊥AB,∠CDB=30°,CD=2$\sqrt{3}$,则S阴影=$\frac{2π}{3}$.
如图,AB是⊙O直径,CD⊥AB,∠CDB=30°,CD=2$\sqrt{3}$,则S阴影=$\frac{2π}{3}$.
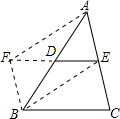 完成下列证明过程,求证:三角形的中位线平行于三角形的第三边,并且等于第三边的一半.
完成下列证明过程,求证:三角形的中位线平行于三角形的第三边,并且等于第三边的一半.