题目内容
10.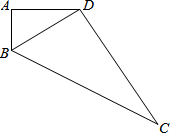 已知,如图,∠A=90°,AB=3,AD=4,CD=12,BC=13.
已知,如图,∠A=90°,AB=3,AD=4,CD=12,BC=13.(1)求BD的长;
(2)判断△BCD是什么三角形,并说明理由;
(3)求四边形ABCD的面积?
分析 (1)在直角△ABD中,根据勾股定理求得BD的长度;
(2)在△BCD中,求得BC2=BD2+CD2,利用勾股定理的逆定理可以判定△BCD是直角三角形;
(3)利用直角三角形的面积公式进行计算即可.
解答 解:(1)如图,在△ABD中,AB=3,AD=4,∠A=90°,
∴由勾股定理得 BD=$\sqrt{A{B}^{2}+A{D}^{2}}=\sqrt{{3}^{2}+{4}^{2}}$=5,即BD=5;
(2)△BCD是直角三角形.理由如下:
在△BCD中,BC=13,CD=12,BD=5,
∴BC2=169,BD2+CD2=52+122=169,
∴BC2=BD2+CD2,
∴△BCD是直角三角形;
(3)解:四边形ABCD的面积:$\frac{1}{2}$×3×4+$\frac{1}{2}$×5×12=36.
点评 本题考查了勾股定理,关键是根据勾股定理和其逆定理进行分析.注意:勾股定理应用的前提条件是在直角三角形中.

练习册系列答案
 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案
相关题目
18.下列二次根式,能与$\sqrt{3}$合并的是( )
| A. | $\sqrt{18}$ | B. | $\sqrt{20}$ | C. | $\sqrt{48}$ | D. | $\sqrt{\frac{1}{2}}$ |
5.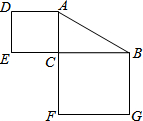 如图,在Rt△ABC中,∠C=90°,若AB=15,则正方形ADEC和正方形BCFG的面积和为( )
如图,在Rt△ABC中,∠C=90°,若AB=15,则正方形ADEC和正方形BCFG的面积和为( )
 如图,在Rt△ABC中,∠C=90°,若AB=15,则正方形ADEC和正方形BCFG的面积和为( )
如图,在Rt△ABC中,∠C=90°,若AB=15,则正方形ADEC和正方形BCFG的面积和为( )| A. | 225 | B. | 200 | C. | 250 | D. | 150 |
19. 如图,AC=AD,BC=BD,则( )
如图,AC=AD,BC=BD,则( )
 如图,AC=AD,BC=BD,则( )
如图,AC=AD,BC=BD,则( )| A. | CD垂直平分AD | B. | AB垂直平分CD | C. | CD平分∠ACB | D. | 以上结论均不对 |
 如图,若AB∥CD,CE平分∠DCB,且∠B+∠DAB=180°.证明:∠E=∠3.
如图,若AB∥CD,CE平分∠DCB,且∠B+∠DAB=180°.证明:∠E=∠3. 已知,一次函数y=-$\frac{3}{4}$x+6的图象与x轴交于A,与y轴交于C,以O,A,C为顶点在第一象限作矩形OABC.
已知,一次函数y=-$\frac{3}{4}$x+6的图象与x轴交于A,与y轴交于C,以O,A,C为顶点在第一象限作矩形OABC.