题目内容
8. 已知如图,CO、CB是⊙O′的弦,⊙O′与坐标系x、y轴交于B、A两点,∠OCB=60°,点A的坐标为(0,1),则⊙O′的弦OB的长为( )
已知如图,CO、CB是⊙O′的弦,⊙O′与坐标系x、y轴交于B、A两点,∠OCB=60°,点A的坐标为(0,1),则⊙O′的弦OB的长为( )| A. | 1 | B. | 2 | C. | $\sqrt{3}$ | D. | 2$\sqrt{3}$ |
分析 首先连接AB,由∠AOB=90°,可得AB是直径,又由∠OAB=∠OCB=60°,然后根据含30°的直角三角形的性质,求得AB的长,然后根据勾股定理,求得OB的长.
解答  解:连接AB,
解:连接AB,
∵∠AOB=90°,
∴AB是直径,
∵∠OAB=∠OCB=60°,
∴∠ABO=30°,
∵点A的坐标为(0,1),
∴OA=1,
∴AB=2OA=2,
∴OB=$\sqrt{A{B}^{2}-O{A}^{2}}$=$\sqrt{3}$.
故选C.
点评 此题考查了圆周角定理以及勾股定理.注意准确作出辅助线是解此题的关键.

练习册系列答案
相关题目
19. 如图,设△ABC和△CDE都是等边三角形,且∠EBD=65°,则∠AEB的度数是( )
如图,设△ABC和△CDE都是等边三角形,且∠EBD=65°,则∠AEB的度数是( )
 如图,设△ABC和△CDE都是等边三角形,且∠EBD=65°,则∠AEB的度数是( )
如图,设△ABC和△CDE都是等边三角形,且∠EBD=65°,则∠AEB的度数是( )| A. | 115° | B. | 120° | C. | 125° | D. | 130° |
13.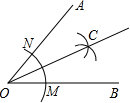 如图,用直尺和圆规作∠AOB的平分线的示意图如图所示,则下列选项中,能说明图中所作出的射线OC是∠AOB的平分线的依据是( )
如图,用直尺和圆规作∠AOB的平分线的示意图如图所示,则下列选项中,能说明图中所作出的射线OC是∠AOB的平分线的依据是( )
 如图,用直尺和圆规作∠AOB的平分线的示意图如图所示,则下列选项中,能说明图中所作出的射线OC是∠AOB的平分线的依据是( )
如图,用直尺和圆规作∠AOB的平分线的示意图如图所示,则下列选项中,能说明图中所作出的射线OC是∠AOB的平分线的依据是( )| A. | SSS | |
| B. | ASA | |
| C. | AAS | |
| D. | 角平分线是哪个的点到这个角两边的距离相等 |
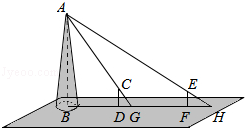 如图,某水平地面上建筑物的高度为AB,在点D和点F处分别竖立高是2米的标杆CD和EF,两标杆相隔52米,并且建筑物AB、标杆CD和EF在同一竖直平面内,从标杆CD后退2米到点G处,在G处测得建筑物顶端A和标杆顶端C在同一条直线上;从标杆FE后退4米到点H处,在H处测得建筑物顶端A和标杆顶端E在同一条直线上,求建筑物的高.
如图,某水平地面上建筑物的高度为AB,在点D和点F处分别竖立高是2米的标杆CD和EF,两标杆相隔52米,并且建筑物AB、标杆CD和EF在同一竖直平面内,从标杆CD后退2米到点G处,在G处测得建筑物顶端A和标杆顶端C在同一条直线上;从标杆FE后退4米到点H处,在H处测得建筑物顶端A和标杆顶端E在同一条直线上,求建筑物的高. 如图,已知△ABC中,∠ABC=45°,F是高AD和BE的交点,CD=3,则线段DF的长度为3.
如图,已知△ABC中,∠ABC=45°,F是高AD和BE的交点,CD=3,则线段DF的长度为3. 如图,∠B=∠D,∠BAC=∠DAC,求证:△ABC≌△ADC.
如图,∠B=∠D,∠BAC=∠DAC,求证:△ABC≌△ADC. 如图,已知△ABC中,AB=6,AC=9,AD⊥BC于D,M为AD上任一点,则MC2-MB2=45.
如图,已知△ABC中,AB=6,AC=9,AD⊥BC于D,M为AD上任一点,则MC2-MB2=45.