题目内容
19. 如图,设△ABC和△CDE都是等边三角形,且∠EBD=65°,则∠AEB的度数是( )
如图,设△ABC和△CDE都是等边三角形,且∠EBD=65°,则∠AEB的度数是( )| A. | 115° | B. | 120° | C. | 125° | D. | 130° |
分析 根据等边三角形性质得出AC=BC,CE=CD,∠BAC=60°,∠ACB=∠ECD=60°,求出∠ACE=∠BCD,证△ACE≌△BCD,根据全等三角形的性质得出∠CAE=∠CBD,求出∠ABE+∠BAE=55°,根据三角形内角和定理求出即可.
解答 解:∵△ABC和△CDE都是等边三角形,
∴AC=BC,CE=CD,∠BAC=60°,∠ACB=∠ECD=60°,
∴∠ACB-∠ECB=∠ECD-∠ECB,
∴∠ACE=∠BCD,
在△ACE和△BCD中,
$\left\{\begin{array}{l}{AC=BC}\\{∠ACE=∠BCD}\\{CE=CD}\end{array}\right.$,
∴△ACE≌△BCD(SAS),
∴∠CAE=∠CBD,
∵∠EBD=65°,
∴65°-∠EBC=60°-∠BAE,
∴65°-(60°-∠ABE)=60°-∠BAE,
∴∠ABE+∠BAE=55°,
∴∠AEB=180°-(∠ABE+∠BAE)=125°.
故选C.
点评 本题考查了全等三角形的性质和判定,三角形内角和定理,等边三角形的性质的应用,能求出∠CAE=∠CBD是解此题的关键,难度适中.

练习册系列答案
 高效智能课时作业系列答案
高效智能课时作业系列答案 捷径训练检测卷系列答案
捷径训练检测卷系列答案
相关题目
10.观察下列单项式的排列规律:3x,-7x2,11x3,-15x4,19x5,…,照这样排列第10个单项式应是( )
| A. | 39x10 | B. | -39x10 | C. | -43x10 | D. | 43x10 |
11.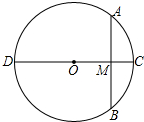 如图,⊙O的直径CD=10cm,AB是⊙O的弦,AB⊥CD,垂足为M,OM:OC=3:5,则AB的长为( )
如图,⊙O的直径CD=10cm,AB是⊙O的弦,AB⊥CD,垂足为M,OM:OC=3:5,则AB的长为( )
 如图,⊙O的直径CD=10cm,AB是⊙O的弦,AB⊥CD,垂足为M,OM:OC=3:5,则AB的长为( )
如图,⊙O的直径CD=10cm,AB是⊙O的弦,AB⊥CD,垂足为M,OM:OC=3:5,则AB的长为( )| A. | $\sqrt{91}$cm | B. | 8cm | C. | 6cm | D. | 4cm |
8. 已知如图,CO、CB是⊙O′的弦,⊙O′与坐标系x、y轴交于B、A两点,∠OCB=60°,点A的坐标为(0,1),则⊙O′的弦OB的长为( )
已知如图,CO、CB是⊙O′的弦,⊙O′与坐标系x、y轴交于B、A两点,∠OCB=60°,点A的坐标为(0,1),则⊙O′的弦OB的长为( )
 已知如图,CO、CB是⊙O′的弦,⊙O′与坐标系x、y轴交于B、A两点,∠OCB=60°,点A的坐标为(0,1),则⊙O′的弦OB的长为( )
已知如图,CO、CB是⊙O′的弦,⊙O′与坐标系x、y轴交于B、A两点,∠OCB=60°,点A的坐标为(0,1),则⊙O′的弦OB的长为( )| A. | 1 | B. | 2 | C. | $\sqrt{3}$ | D. | 2$\sqrt{3}$ |
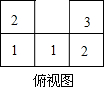 如图,是一个由小立方体搭成的几何体的俯视图(从上面看),小正方形中的数字表示在该位置的小立方体的个数,请画出它的主视图(从正面看)和左视图(从左面看).
如图,是一个由小立方体搭成的几何体的俯视图(从上面看),小正方形中的数字表示在该位置的小立方体的个数,请画出它的主视图(从正面看)和左视图(从左面看).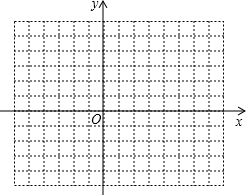 如图,已知△ABC的三个顶点的坐标分别为A(-2,3)、B(-6,0)、C(-1,0).
如图,已知△ABC的三个顶点的坐标分别为A(-2,3)、B(-6,0)、C(-1,0).