题目内容
8.为迎接省运会主板方准备筹建一个奥林匹克体育公园,决定购进A、B两种绿化树共1000棵进行栽种,其中要求A种绿化树的棵树不超过600棵,已知,A种绿化树每棵180元,B种绿化树每棵220元,设购进A种绿化树x棵,购进两种绿化树的总费用为y(1)请求出y关于x的函数关系式,并指出自变量x的取值范围;
(2)请计算出怎样购买才能使总费用最少,最少总费用是多少?
分析 (1)根据总费用=A种绿化树的费用+B种绿化树的费用,即可解答;
(2)得出函数关系后根据(1)的自变量的取值范围和函数的性质判断出租金最少的方案.
解答 解:(1)y=180x+220(1000-x)=-40x+220000,
∵要求A种绿化树的棵树不超过600棵,
∴0<x≤600.
(2)y=-40x+220000,
∵k=-40<0,
∴y随x的增大而减小,
∵0<x≤600,
∴当x=600时,y有最小值,最少费用为:-40×600+220000=186000(元).
点评 本题考查了一次函数的应用,解决本题的关键是列出函数关系式,利用一次函数的性质进行解答.

练习册系列答案
 高中必刷题系列答案
高中必刷题系列答案
相关题目
 如图,AB=DF,AC=DE,BE=FC,∠A与∠D相等吗?说明你的理由.
如图,AB=DF,AC=DE,BE=FC,∠A与∠D相等吗?说明你的理由.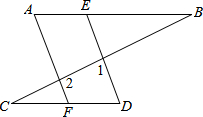 已知:如图,∠A=∠D,∠B=∠C,那么∠1与∠2互补吗?为什么?
已知:如图,∠A=∠D,∠B=∠C,那么∠1与∠2互补吗?为什么?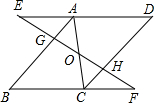 如图,已知AB∥CD,AB=CD,O是AC的中点,过O作直线分别交直线AD、BC于E、F,交线段AB、CD于G、H
如图,已知AB∥CD,AB=CD,O是AC的中点,过O作直线分别交直线AD、BC于E、F,交线段AB、CD于G、H