题目内容
13.计算:(1)(5-$\sqrt{48}$-6$\sqrt{27}$+4$\sqrt{15}$)+$\sqrt{3}$-4$\sqrt{5}$
(2)($\sqrt{3}+1$)($\sqrt{3}-1$)-$\sqrt{(-3)^{2}}$-($\sqrt{2}-1$)0+$\frac{1}{\sqrt{2}-1}$.
分析 (1)先对原式化简,然后合并同类项即可解答本题;
(2)根据平方差公式、零指数幂、分母有理化可以解答本题.
解答 解:(1)(5-$\sqrt{48}$-6$\sqrt{27}$+4$\sqrt{15}$)+$\sqrt{3}$-4$\sqrt{5}$
=5-4$\sqrt{3}$-18$\sqrt{3}$+4$\sqrt{15}$+$\sqrt{3}$-4$\sqrt{5}$
=5-21$\sqrt{3}$+4$\sqrt{15}$-4$\sqrt{5}$;
(2)($\sqrt{3}+1$)($\sqrt{3}-1$)-$\sqrt{(-3)^{2}}$-($\sqrt{2}-1$)0+$\frac{1}{\sqrt{2}-1}$
=3-1-3-1+$\sqrt{2}$+1
=$\sqrt{2}$-1.
点评 本题考查二次根式的混合运算、零指数幂,解题的关键是明确二次根式的混合运算的计算方法,知道除零以外任何数的零次幂都等于1.

练习册系列答案
相关题目
18.下列等式从左到右的变形,是因式分解的是( )
| A. | a(x-y)=ax-ay | B. | x2-2x+3=x(x-2)+3 | C. | (x-1)(x+4)=x2+3x-4 | D. | x3-2x2+x=x(x-1)2 |
5.要使二次根式$\sqrt{3-m}$有意义,则m的取值范围为( )
| A. | m<3 | B. | m≤3 | C. | m>3 | D. | m≥3 |
3.已知,点A(-6,y1)和点B(1,y2)都在直线y=-$\frac{1}{2}$x-1上,那么y1与y2的大小关系是( )
| A. | y1>y2 | B. | y1=y2 | C. | y1<y2 | D. | 不确定 |
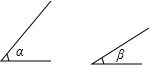 如图,已知∠α、∠β.
如图,已知∠α、∠β. 如图,在平面直角坐标系中,矩形OABC的对角线OB、AC相交于点D,且BE∥AC,CE∥OB.
如图,在平面直角坐标系中,矩形OABC的对角线OB、AC相交于点D,且BE∥AC,CE∥OB. 如图,在矩形ABCD中,AB=l,BC=2,点E在AD上,且ED=3AE.
如图,在矩形ABCD中,AB=l,BC=2,点E在AD上,且ED=3AE.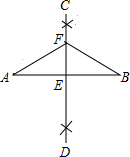 如图,已知线段AB,分别以点A和点B为圆心,大于$\frac{1}{2}$AB的长为半径作弧,两弧相交于C、D两点,作直线CD交AB于点E,在直线CD上任取一点F,连接FA,FB.若FA=5,则FB=5.
如图,已知线段AB,分别以点A和点B为圆心,大于$\frac{1}{2}$AB的长为半径作弧,两弧相交于C、D两点,作直线CD交AB于点E,在直线CD上任取一点F,连接FA,FB.若FA=5,则FB=5.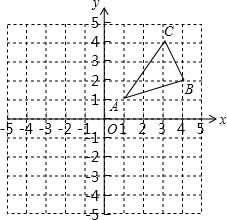 如图,△ABC三个顶点的坐标分别为A(1,1),B(4,2),C(3,4)
如图,△ABC三个顶点的坐标分别为A(1,1),B(4,2),C(3,4)