题目内容
19.下列等式从左到右的变形,属于因式分解的是( )| A. | (x+3)(x-3)=x2-9 | B. | x2-4+3x=(x+2)(x-2)+3x | ||
| C. | (x-1)2=x2-2x+1 | D. | xy2-x2y=xy(y-x) |
分析 根据因式分解是把一个多项式转化成几个整式积的形式,可得答案.
解答 解:A、是整式的乘法,故A错误;
B、没把一个多项式转化成几个整式积的形式,故B错误;
C、是整式的乘法,故C错误;
D、把一个多项式转化成几个整式积的形式,故D正确;
故选:D.
点评 本题考查了因式分解的意义,因式分解是把一个多项式转化成几个整式积的形式,注意正确区分因式分解与整式的乘法是解题关键.

练习册系列答案
 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案
相关题目
10.为了解某校初二年级400名学生的身高情况,从中抽取了50名学生的身高进行统计分析,在这个问题中,样本是指( )
| A. | 50名学生 | B. | 50名学生的身高 | C. | 400名学生 | D. | 400名学生的身高 |
14.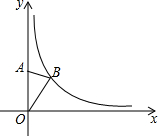 如图,在平面直角坐标系中,点A是y轴正半轴上的一个定点,点B是反比例函数y=$\frac{k}{x}$(k为常数)在第一象限内图象上的一个动点.当点B的纵坐标逐渐增大时,△OAB的面积( )
如图,在平面直角坐标系中,点A是y轴正半轴上的一个定点,点B是反比例函数y=$\frac{k}{x}$(k为常数)在第一象限内图象上的一个动点.当点B的纵坐标逐渐增大时,△OAB的面积( )
 如图,在平面直角坐标系中,点A是y轴正半轴上的一个定点,点B是反比例函数y=$\frac{k}{x}$(k为常数)在第一象限内图象上的一个动点.当点B的纵坐标逐渐增大时,△OAB的面积( )
如图,在平面直角坐标系中,点A是y轴正半轴上的一个定点,点B是反比例函数y=$\frac{k}{x}$(k为常数)在第一象限内图象上的一个动点.当点B的纵坐标逐渐增大时,△OAB的面积( )| A. | 逐渐减小 | B. | 逐渐增大 | C. | 先增大后减小 | D. | 不变 |
11.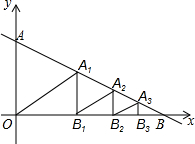 如图,已知直线y=-$\frac{1}{2}$x+2与x轴交于点B,与y轴交于点A.过线段AB的中点A1做A1B1⊥x轴于点B1,过线段A1B的中点A2作A2B2⊥x轴于点B2,过线段A2B的中点A3作A3B3⊥x轴于点B3…,以此类推,则△AnBnBn-1的面积为( )
如图,已知直线y=-$\frac{1}{2}$x+2与x轴交于点B,与y轴交于点A.过线段AB的中点A1做A1B1⊥x轴于点B1,过线段A1B的中点A2作A2B2⊥x轴于点B2,过线段A2B的中点A3作A3B3⊥x轴于点B3…,以此类推,则△AnBnBn-1的面积为( )
 如图,已知直线y=-$\frac{1}{2}$x+2与x轴交于点B,与y轴交于点A.过线段AB的中点A1做A1B1⊥x轴于点B1,过线段A1B的中点A2作A2B2⊥x轴于点B2,过线段A2B的中点A3作A3B3⊥x轴于点B3…,以此类推,则△AnBnBn-1的面积为( )
如图,已知直线y=-$\frac{1}{2}$x+2与x轴交于点B,与y轴交于点A.过线段AB的中点A1做A1B1⊥x轴于点B1,过线段A1B的中点A2作A2B2⊥x轴于点B2,过线段A2B的中点A3作A3B3⊥x轴于点B3…,以此类推,则△AnBnBn-1的面积为( )| A. | $\frac{1}{{2}^{n-1}}$ | B. | $\frac{1}{{2}^{n}}$ | C. | $\frac{1}{{4}^{n-1}}$ | D. | $\frac{1}{{4}^{n}}$ |
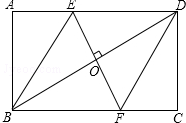 如图,在矩形ABCD中,边AB的长为3,点E,F分别在AD,BC上,连接BE,DF,EF,BD.若四边形BEDF是菱形,且EF=AE+FC,则边BC的长为3$\sqrt{3}$.
如图,在矩形ABCD中,边AB的长为3,点E,F分别在AD,BC上,连接BE,DF,EF,BD.若四边形BEDF是菱形,且EF=AE+FC,则边BC的长为3$\sqrt{3}$. 如图,在Rt△ABC中,∠C=90°,BC=3cm,AC=4cm,那么sinA=$\frac{3}{5}$.
如图,在Rt△ABC中,∠C=90°,BC=3cm,AC=4cm,那么sinA=$\frac{3}{5}$. 如图,在Rt△AOB中,OA=OB=4,⊙O的半径为1,点P是AB边上的动点,过点P作⊙O的一条切线PQ(点Q为切点),则线段PQ长度的最小值为$\sqrt{7}$.
如图,在Rt△AOB中,OA=OB=4,⊙O的半径为1,点P是AB边上的动点,过点P作⊙O的一条切线PQ(点Q为切点),则线段PQ长度的最小值为$\sqrt{7}$.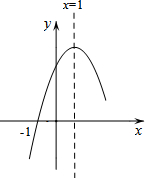 如图,二次函数y=ax2+bx+c(a≠0)的图象与x轴交于A、B两点,与y轴交于C点,且对称轴为直线x=1,点B坐标为(-1,0).则下面的四个结论:①2a+b=0;②8a+c<0;③abc>0;④当y<0时,x<-1或x>2,⑤对任意实数m,m(am+b)≤a+b.其中正确的结论有( )个.
如图,二次函数y=ax2+bx+c(a≠0)的图象与x轴交于A、B两点,与y轴交于C点,且对称轴为直线x=1,点B坐标为(-1,0).则下面的四个结论:①2a+b=0;②8a+c<0;③abc>0;④当y<0时,x<-1或x>2,⑤对任意实数m,m(am+b)≤a+b.其中正确的结论有( )个.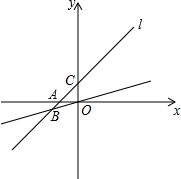 直线l经过(2,3)和(-2,-1)两点,它还与x轴交于A点,与y轴交于C点,与经过原点的直线OB交于第三象限的B点,且∠ABO=30°.求:
直线l经过(2,3)和(-2,-1)两点,它还与x轴交于A点,与y轴交于C点,与经过原点的直线OB交于第三象限的B点,且∠ABO=30°.求: