题目内容
6.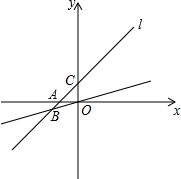 直线l经过(2,3)和(-2,-1)两点,它还与x轴交于A点,与y轴交于C点,与经过原点的直线OB交于第三象限的B点,且∠ABO=30°.求:
直线l经过(2,3)和(-2,-1)两点,它还与x轴交于A点,与y轴交于C点,与经过原点的直线OB交于第三象限的B点,且∠ABO=30°.求:(1)点A、C的坐标;
(2)点B的坐标.
分析 (1)用待定系数法求出AC的解析式,分别求出点A、C的坐标即可;
(2)根据勾股定理求出AC的长,作OD⊥AC于D,BF⊥y轴于F,求出OF、BF的长即可.
解答 解:(1)设直线l的解析式为:y=kx+b,
则$\left\{\begin{array}{l}{2k+b=3}\\{-2k+b=-1}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=1}\\{b=1}\end{array}\right.$,
∴直线l的解析式为:y=x+1,
则点A的坐标(-1,0),B(0,1).
(2)作OD⊥AC于D,BF⊥y轴于F,
∵OA=1,OC=1,
∴AC=$\sqrt{2}$,
则OD=AD=CD=$\frac{\sqrt{2}}{2}$,
在Rt△BOD中,∠ABO=30°,
BD=$\frac{\sqrt{6}}{2}$,则BC=$\frac{\sqrt{6}+\sqrt{2}}{2}$,
|BF|=|CF|=$\frac{\sqrt{2}}{2}$•$\frac{\sqrt{6}+\sqrt{2}}{2}$=$\frac{\sqrt{3}+1}{2}$,
|OF|=$\frac{\sqrt{3}+1}{2}$-1=$\frac{\sqrt{3}-1}{2}$,
∵B在第三象限,
∴点B的坐标为:(-$\frac{\sqrt{3}+1}{2}$,-$\frac{\sqrt{3}-1}{2}$).
点评 本题考查的是一次函数的知识,正确运用勾股定理和待定系数法求解析式是解题的关键,解答时,注意锐角三角函数的运用.

练习册系列答案
 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案
相关题目
19.下列等式从左到右的变形,属于因式分解的是( )
| A. | (x+3)(x-3)=x2-9 | B. | x2-4+3x=(x+2)(x-2)+3x | ||
| C. | (x-1)2=x2-2x+1 | D. | xy2-x2y=xy(y-x) |
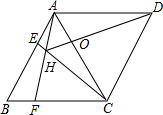 如图,菱形ABCD中,AB=AC,点E、F分别为边AB、BC上的点,且AE=BF,连接CE、AF交于点H,则下列结论:①△ABF≌△CAE;②∠AHC=120°;③△AEH∽△CEA;④AE•AD=AH•AF;其中结论正确的个数是( )
如图,菱形ABCD中,AB=AC,点E、F分别为边AB、BC上的点,且AE=BF,连接CE、AF交于点H,则下列结论:①△ABF≌△CAE;②∠AHC=120°;③△AEH∽△CEA;④AE•AD=AH•AF;其中结论正确的个数是( ) 如图,点P在半径为3的⊙O内,OP=$\sqrt{3}$,点A为⊙O上一动点,弦AB过点P,则AB最长为6,AB最短为2$\sqrt{6}$.
如图,点P在半径为3的⊙O内,OP=$\sqrt{3}$,点A为⊙O上一动点,弦AB过点P,则AB最长为6,AB最短为2$\sqrt{6}$. ,当x=1时,请你选择一个恰当的y值代入求值.
,当x=1时,请你选择一个恰当的y值代入求值. 在实数范围内有意义,则x的取值范围是( )
在实数范围内有意义,则x的取值范围是( ) B.
B.  C.
C.  D. 以上都不对
D. 以上都不对