题目内容
7．
如图，在Rt△ABC中，∠C=90°，BC=3cm，AC=4cm，那么sinA=$\frac{3}{5}$．
分析 根据勾股定理求出斜边AB的长，根据正弦的概念求出sinA．
解答 解：∵，∠C=90°，BC=3，AC=4，
由勾股定理得，AB=5，
sinA=$\frac{BC}{AB}$=$\frac{3}{5}$．
故答案为：$\frac{3}{5}$．
点评 本题考查锐角三角函数的定义及运用，在直角三角形中，锐角的正弦为对边比斜边，余弦为邻边比斜边，正切为对边比邻边．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
如图，等腰三角形ABC的周长为21，底边BC的长为5，腰AB的垂直平分线交AB于点D，交AC于点E，连接BE，则三角形BEC的周长为（ ）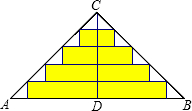
如图，△ABC是一张直角三角形彩色纸，AC=15cm，BC=20cm．若将斜边上的高CD 分成n等分，然后裁出（n-1）张宽度相等的长方形纸条．则这（n-1）张纸条的面积和是$\frac{150（n-1）}{n}$cm2．
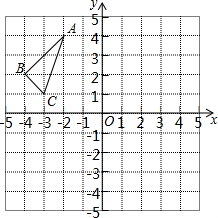△ABC在平面直角坐标系中的位置如图所示，其中每个小正方形的边长为1个单位长度．
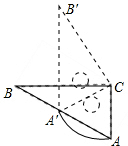如图，Rt△ABC中，∠B=30°，斜边AB长12为cm，绕直角顶点C顺时针旋转，当点A落在AB边上的A′处，则弧AA′的长为2π cm．（结果保留π）
12．不等式组$\left\{\begin{array}{l}{x+1＞0}\\{x-2≤-1}\end{array}\right.$中的两个不等式的解集在同一个数轴上表示正确的是（ ）
| A． |  | B． |  | C． |  | D． |  |
19．下列等式从左到右的变形，属于因式分解的是（ ）
| A． | （x+3）（x-3）=x2-9 | B． | x2-4+3x=（x+2）（x-2）+3x | ||
| C． | （x-1）2=x2-2x+1 | D． | xy2-x2y=xy（y-x） |
16．
如图，该几何体的俯视图是（ ）
如图，该几何体的俯视图是（ ）| A． |  | B． |  | C． |  | D． |  |
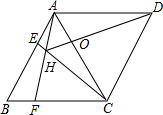如图，菱形ABCD中，AB=AC，点E、F分别为边AB、BC上的点，且AE=BF，连接CE、AF交于点H，则下列结论：①△ABF≌△CAE；②∠AHC=120°；③△AEH∽△CEA；④AE•AD=AH•AF；其中结论正确的个数是（ ）