题目内容
15.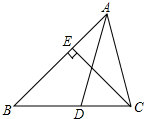 如图,AD是△ABC的角平分线,CE是△ABC的高,∠BAC=64°,∠BCE=40°,求∠ADC的度数.
如图,AD是△ABC的角平分线,CE是△ABC的高,∠BAC=64°,∠BCE=40°,求∠ADC的度数.
分析 首先根据∠BAC=64°,AD是△ABC的角平分线,求出∠BAD的度数是多少;然后根据CE是△ABC的高,求出∠B=50°;最后根据三角形的外角的性质,求出∠ADC的度数是多少即可.
解答 解:∵∠BAC=64°,AD是△ABC的角平分线,
∴∠BAD=∠DAC=64°÷2=32°,
∵CE是△ABC的高.
∴∠CEB=90°,
∵∠BCE=40°,
∴∠B=90°-40°=50°,
∴∠ADC=∠BAD+∠B=32°+50°=82°,
即∠ADC的度数是82°.
点评 (1)此题主要考查了三角形的内角和定理,要熟练掌握,解答此题的关键是要明确:三角形的内角和是180°.
(2)此题主要考查了三角形的外角性质,要熟练掌握,解答此题的关键是要明确:①三角形的外角和为360°.②三角形的一个外角等于和它不相邻的两个内角的和.③三角形的一个外角大于和它不相邻的任何一个内角.

练习册系列答案
相关题目
6.根据下面表格中的取值,方程x2+x-3=0有一个根的近似值(精确到0.1)是( )
| x | 1.2 | 1.3 | 1.4 | 1.5 |
| x2+x-3 | -0.36 | -0.01 | 0.36 | 0.75 |
| A. | 1.5 | B. | 1.2 | C. | 1.3 | D. | 1.4 |
20.已知一次函数y=(m+4)x+m-2的图象不过第二象限,则m的取值范围是( )
| A. | m>-4 | B. | m<2 | C. | -4<m≤2 | D. | m>2 |
5.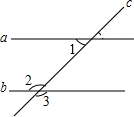 如图,a∥b,∠3=135°,则∠1的度数是( )
如图,a∥b,∠3=135°,则∠1的度数是( )
 如图,a∥b,∠3=135°,则∠1的度数是( )
如图,a∥b,∠3=135°,则∠1的度数是( )| A. | 45° | B. | 55° | C. | 65° | D. | 75° |
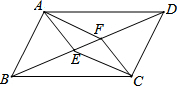 已知:如图,在?ABCD中,∠BAD和∠BCD的平分线AE、CF分别与对角线BD相交于点E,F.证明:四边形AECF是平行四边形.
已知:如图,在?ABCD中,∠BAD和∠BCD的平分线AE、CF分别与对角线BD相交于点E,F.证明:四边形AECF是平行四边形.