题目内容
20.已知一次函数y=(m+4)x+m-2的图象不过第二象限,则m的取值范围是( )| A. | m>-4 | B. | m<2 | C. | -4<m≤2 | D. | m>2 |
分析 根据一次函数的图象不经过第二象限列出关于m的不等式组,求出m的取值范围即可.
解答 解:∵一次函数y=mx+2m-1的图象不经过第二象限,
∴$\left\{\begin{array}{l}{m+4>0}\\{m-2≤0}\end{array}\right.$,
解得:-4<m≤2.
故选C.
点评 本题考查的是一次函数的图象与系数的关系,熟知一次函数y=kx+b(k≠0)中,当k>0,b<0时,函数的图象经过一三四象限是解答此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
11.在数-3,-2,0,3中,大小在-1和2之间的数是( )
| A. | -3 | B. | -2 | C. | 0 | D. | 3 |
11.在8点30分时,时针上的时针与分针之间的夹角为( )
| A. | 85度 | B. | 75度 | C. | 70度 | D. | 60度 |
10.甲、乙两人相距50千米,若同向而行,乙10小时可追上甲;若相向而行,2小时两人相遇.设甲、乙两人每小时分别走x千米、y千米,则可列出方程组是( )
| A. | $\left\{\begin{array}{l}{10x-10y=50}\\{2x+2y=50}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{10x+10y=50}\\{2x+2y=50}\end{array}\right.$ | ||
| C. | $\left\{\begin{array}{l}{10y-10x=50}\\{2x+2y=50}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{10x-10y=50}\\{2x-2y=50}\end{array}\right.$ |
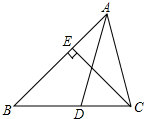 如图,AD是△ABC的角平分线,CE是△ABC的高,∠BAC=64°,∠BCE=40°,求∠ADC的度数.
如图,AD是△ABC的角平分线,CE是△ABC的高,∠BAC=64°,∠BCE=40°,求∠ADC的度数.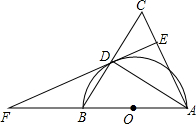 如图,在△ABC中,AB=AC,以AB为直径作半圆⊙O,交BC于点D,连接AD,过点D作DE⊥AC,垂足为点E,交AB的延长线于点F.
如图,在△ABC中,AB=AC,以AB为直径作半圆⊙O,交BC于点D,连接AD,过点D作DE⊥AC,垂足为点E,交AB的延长线于点F.