题目内容
3.分式①$\frac{{x}^{2}+{y}^{2}}{x-y}$+$\frac{2xy}{y-x}$;②$\frac{{x}^{2}-{y}^{2}}{4xy}$-$\frac{{x}^{2}+{y}^{2}}{4xy}$;③$\frac{{a}^{2}}{a-b}$+$\frac{{a}^{2}-a+b}{b-a}$中,计算结果是整式的序号为①③.分析 各项化简得到结果,即可做出判断.
解答 解:①原式=$\frac{{x}^{2}+{y}^{2}-2xy}{x-y}$=$\frac{(x-y)^{2}}{x-y}$=x-y,满足题意;
②原式=$\frac{{x}^{2}-{y}^{2}-{x}^{2}-{y}^{2}}{4xy}$=$\frac{-2{y}^{2}}{4xy}$=-$\frac{y}{2x}$,不合题意;
③原式=$\frac{{a}^{2}-{a}^{2}+a-b}{a-b}$=1,符合题意,
则计算结果为整式的序号为①③.
故答案为:①③.
点评 此题考查了分式的加减法,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
11.在8点30分时,时针上的时针与分针之间的夹角为( )
| A. | 85度 | B. | 75度 | C. | 70度 | D. | 60度 |
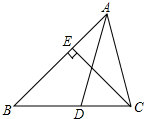 如图,AD是△ABC的角平分线,CE是△ABC的高,∠BAC=64°,∠BCE=40°,求∠ADC的度数.
如图,AD是△ABC的角平分线,CE是△ABC的高,∠BAC=64°,∠BCE=40°,求∠ADC的度数.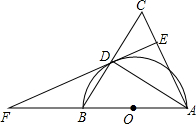 如图,在△ABC中,AB=AC,以AB为直径作半圆⊙O,交BC于点D,连接AD,过点D作DE⊥AC,垂足为点E,交AB的延长线于点F.
如图,在△ABC中,AB=AC,以AB为直径作半圆⊙O,交BC于点D,连接AD,过点D作DE⊥AC,垂足为点E,交AB的延长线于点F.