题目内容
9.若函数y=4x+b的图象与两坐标轴围成的三角形面积为2,则b=±4.分析 先令x=0,求出y的值,再令y=0求出x的值即可得出直线与坐标轴的交点,再利用三角形的面积公式求解即可.
解答 解:∵令x=0,则y=b;令y=0,则x=-$\frac{b}{4}$,
∴函数y=4x+b与xy轴的交点分别为(-$\frac{b}{4}$,0)(0,b).
∵函数y=4x+b的图象与两坐标轴围成的三角形面积为2,
∴$\frac{1}{2}$|b|•|-$\frac{b}{4}$|=2,解得b=±4.
故答案为:±4;
点评 本题考查的是一次函数图象上点的坐标特点,熟知一次函数图象上各点的坐标一定适合此函数的解析式是解答此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
19.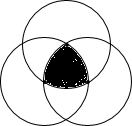 如图,分别以边长为2的正三角形的顶点为圆心,2为半径作三个圆,则这三个圆围成的阴影部分面积是( )
如图,分别以边长为2的正三角形的顶点为圆心,2为半径作三个圆,则这三个圆围成的阴影部分面积是( )
 如图,分别以边长为2的正三角形的顶点为圆心,2为半径作三个圆,则这三个圆围成的阴影部分面积是( )
如图,分别以边长为2的正三角形的顶点为圆心,2为半径作三个圆,则这三个圆围成的阴影部分面积是( )| A. | 2π | B. | 2π-$\sqrt{3}$ | C. | 2π-2$\sqrt{3}$ | D. | 2π-3$\sqrt{3}$ |
4.下列语句叙述正确的个数是( )
①横坐标与纵坐标互为相反数的点在直线y=-x上;
②点P(2,0)在y轴上;
③若点P的坐标为(a,b),且ab=0,则P点是坐标原点;
④函数y=1-x中y随x的增大而增大.
①横坐标与纵坐标互为相反数的点在直线y=-x上;
②点P(2,0)在y轴上;
③若点P的坐标为(a,b),且ab=0,则P点是坐标原点;
④函数y=1-x中y随x的增大而增大.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
14.函数y=$\frac{x-1}{\sqrt{x-2}}$中自变量x的取值范围是( )
| A. | x>2 | B. | x≠2 | C. | x≥2且x≠1 | D. | x为任意实数 |
18.已知a+$\frac{1}{a}$=$\sqrt{5}$,则a-$\frac{1}{a}$=( )
| A. | 1 | B. | -1 | C. | ±1 | D. | -$\sqrt{5}$ |
19. 如图,在菱形ABCD中,EF⊥AC于点G,分别交AD及CB的延长线于点E、F交AB于点H,AH:FB=1:2,则AG:GC的值为( )
如图,在菱形ABCD中,EF⊥AC于点G,分别交AD及CB的延长线于点E、F交AB于点H,AH:FB=1:2,则AG:GC的值为( )
 如图,在菱形ABCD中,EF⊥AC于点G,分别交AD及CB的延长线于点E、F交AB于点H,AH:FB=1:2,则AG:GC的值为( )
如图,在菱形ABCD中,EF⊥AC于点G,分别交AD及CB的延长线于点E、F交AB于点H,AH:FB=1:2,则AG:GC的值为( )| A. | $\frac{1}{3}$ | B. | $\frac{1}{5}$ | C. | $\frac{2}{5}$ | D. | $\frac{1}{4}$ |
 如图所示是一个几何体从上面看到的图形,中间的数字表示该位置的小立方块的个数,请画出这个几何体从正面和左面看到的图形.
如图所示是一个几何体从上面看到的图形,中间的数字表示该位置的小立方块的个数,请画出这个几何体从正面和左面看到的图形.