题目内容
3.已知直线y=(k+2)x+$\frac{1-k}{2}$的截距为1,那么该直线与x轴的交点坐标为(-1,0).分析 由条件可先求得k的值,再令y=0,可求得直线与x轴的交点坐标.
解答 解:∵y=(k+2)x+$\frac{1-k}{2}$的截距为1,
∴$\frac{1-k}{2}$=1,解得k=-1,
∴直线解析式为y=x+1,
令y=0,可得x+1=0,解得x=-1,
∴直线与x轴的交点坐标为(-1,0),
故答案为:(-1,0).
点评 本题主要考查截距的概念,掌握一次函数y=kx+b中的b为截距是解题的关键.

练习册系列答案
 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案
相关题目
13.如果单项式-x2ym与3xn+1y的和仍然是一个单项式,则m,n的值是( )
| A. | m=1,n=1 | B. | m=2,n=0 | C. | m=1,n=2 | D. | m=2,n=1 |
11.在平面直角坐标系中,点A(-2,4)位于( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
15.已知a、b、c是常数,且a≠0,则关于x的方程ax2+bx+c=0有实数根的条件是( )
| A. | b2-4ac<0 | B. | b2-4ac>0 | C. | b2-4ac≥0 | D. | b2-4ac≤0 |
12.若|a+2|+(b-1)2=0,那么代数式(a+b)2009的值是( )
| A. | 2009 | B. | -2009 | C. | 1 | D. | -1 |
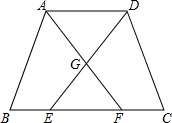 如图,等腰梯形ABCD中,AD∥BC,点E、F在边BC上,且BE=CF,AF与DE相交于点G.求证:GE=GF.
如图,等腰梯形ABCD中,AD∥BC,点E、F在边BC上,且BE=CF,AF与DE相交于点G.求证:GE=GF.