题目内容
5. 已知一次函数y=kx+b(k为常数,k≠0)的图象经过点A(2,2),B(0,1).
已知一次函数y=kx+b(k为常数,k≠0)的图象经过点A(2,2),B(0,1).(1)求该一次函数的解析式,并作出其图象;
(2)当0≤y≤2时,求x的取值范围.
分析 (1)将点A、B的坐标代入一次函数的解析式y=kx+b(k为常数,k≠0),得关于k、b的二元一次方程组,解之即可;
(2)根据函数图象的性质及函数的解析式求x的取值范围或直接利用函数图象确定x的取值范围.
解答 解:(Ⅰ)∵点A(2,2),点B(0,1)在一次函数y=kx+b(k为常数,k≠0)的图象上,
∴$\left\{\begin{array}{l}{2k+b=2}\\{b=1}\end{array}\right.$ 解得$\left\{\begin{array}{l}{k=\frac{1}{2}}\\{b=1}\end{array}\right.$
∴一次函数的解析式为:y=$\frac{1}{2}$x+1
其图象如下图所示:
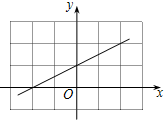
(Ⅱ)∵k=$\frac{1}{2}$>0,
∴一次函数y=$\frac{1}{2}$x+1的函数值y随x的增大而增大.
当y=0时,解得x=-2;当y=2时,x=2.
∴-2≤x≤2.
即:当0≤y≤2时,求x的取值范围是:-2≤x≤2.
点评 本题考查了待定系数法求一次函数的解析式及一次函数图象的画法,关键是要理解函数图象上的点的坐标与函数图象的关系:若点在函数的图象上,那么点的坐标(x,y)就满足函数的解析式y=kx+b.

练习册系列答案
 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案
相关题目
16.下列说法正确的是( )
| A. | 掷一枚均匀的骰子,骰子停止转动后,6点朝上是必然事件 | |
| B. | 了解一批电视机的使用寿命,适合用普查的方式 | |
| C. | “明天降雨的概率为0.5”表示明天有半天都在降雨 | |
| D. | 甲、乙两人在相同条件下各进行10次射击,他们的成绩平均数相同,方差分别是0.4和0.6,则甲的射击成绩较稳定 |
17.某双曲线经过点A(4,-2),则该双曲线一定还经过点( )
| A. | (-4,-2) | B. | (8,1) | C. | (-1,-8) | D. | (-8,1) |
 在“敬老爱亲”活动中,九年级一班全班50名学生做家务的时间(单位:小时)分成5组:A.0.5≤x<1 B.1≤x<1.5 C.1.5≤x<2 D.2≤x<2.5 E.2.5≤x<3,并制成了不完整的条形统计图,其中做家务时间在1.5-2小时的占40%,请根据图中信息解答下列问题:
在“敬老爱亲”活动中,九年级一班全班50名学生做家务的时间(单位:小时)分成5组:A.0.5≤x<1 B.1≤x<1.5 C.1.5≤x<2 D.2≤x<2.5 E.2.5≤x<3,并制成了不完整的条形统计图,其中做家务时间在1.5-2小时的占40%,请根据图中信息解答下列问题:
 如图,已知双曲线y1=$\frac{1}{x}$(x>0),y2=$\frac{4}{x}$(x>0),点P为双曲线y2=$\frac{4}{x}$上的一点,且PA⊥x轴于点A,PB⊥y轴于点B,PA,PB分别交双曲线y1=$\frac{1}{x}$于D,C两点,则△PCD的面积是$\frac{9}{8}$.
如图,已知双曲线y1=$\frac{1}{x}$(x>0),y2=$\frac{4}{x}$(x>0),点P为双曲线y2=$\frac{4}{x}$上的一点,且PA⊥x轴于点A,PB⊥y轴于点B,PA,PB分别交双曲线y1=$\frac{1}{x}$于D,C两点,则△PCD的面积是$\frac{9}{8}$.