题目内容
14.在△ABC中,AB=AC,以AB为直径的⊙O交BC边于点D,连接AD.(1)如图1,求证:CD=BD;
(2)如图2,设⊙O交AC边于点E,过D点作DG⊥AB,垂足为点G,交⊙O于点F,连接DE、EF,求证:∠DEC=∠AEF;
(3)在(2)的条件下,若tan∠CED=$\frac{4}{3}$,OG=$\frac{7}{6}$,求△AED的面积.

分析 (1)由AB是⊙O的直径,根据直径所对的圆周角是直角,可得∠ADB=90°,然后由AB=AC,根据三线合一的性质,可证得CD=BD;
(2)由DG⊥AB,可得$\widehat{AF}$=$\widehat{AD}$,即可得∠ABD=∠AEF,继而证得结论;
(3)首先连接OD,易求得tan∠ADF=$\frac{AG}{DG}$=$\frac{4}{3}$,再设AG=4x,DG=3x,在Rt△ODG中,可得($\frac{7}{6}$)2+(3x)2=(4x-$\frac{7}{6}$)2,即可求得AG,DG的长,然后再过点D作DH⊥CE于点H,求得AE的长,继而求得答案.
解答 (1)证明:∵AB是⊙O的直径,
∴∠ADB=90°,
∴AD⊥BC,
∵AB=AC,
∴CD=BD;
(2)证明:∵AB⊥DF,
∴$\widehat{AF}$=$\widehat{AD}$,
∴∠ABD=∠AEF,
∴∠ABD+∠AED=180°,∠DEC+∠AED=180°,
∴∠DEC=∠ABD=∠AEF;
(3)连接OD,
由(2)知,∠DEC=∠AEF,
∵∠AEF=∠ADF,
∴∠DEC=∠ADF,
∴tan∠ADF=tan∠DEC=$\frac{4}{3}$,
∵AB⊥DG,
∴tan∠ADF=$\frac{AG}{DG}$=$\frac{4}{3}$,
设AG=4x,DG=3x,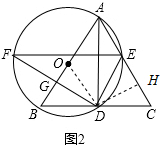
∵OG=$\frac{7}{6}$,
∴OD=OA=4x-$\frac{7}{6}$,
在Rt△ODG中,($\frac{7}{6}$)2+(3x)2=(4x-$\frac{7}{6}$)2,
解得:x=$\frac{4}{3}$,
∴AG=$\frac{16}{3}$,DG=4,
过点D作DH⊥CE于点H,
由(1)可知:AD平分∠BAC,
∴DH=DG=4,AH=AG=$\frac{16}{3}$,
∵tan∠EDC=$\frac{4}{3}$,
∴EH=3,
∴AE=$\frac{16}{3}$-3=$\frac{7}{3}$,
∴S△AED=$\frac{1}{2}$AE•DH=$\frac{1}{2}$×$\frac{7}{3}$×4=$\frac{14}{3}$.
点评 此题属于圆的综合题.考查了圆周角定理、等腰三角形的性质以及锐角三角函数的知识.注意准确作出辅助线、掌握方程思想的应用是解此题的关键.

 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案| x | … | -5 | -4 | -3 | -2 | -1 | … |
| y | … | 3 | -2 | -5 | -6 | -5 | … |
 已知一次函数y=kx+b(k为常数,k≠0)的图象经过点A(2,2),B(0,1).
已知一次函数y=kx+b(k为常数,k≠0)的图象经过点A(2,2),B(0,1). 如图,在梯形ABCD中,AD∥BC,BC=2AD,过点A作AE∥DC交BC于点E.
如图,在梯形ABCD中,AD∥BC,BC=2AD,过点A作AE∥DC交BC于点E.
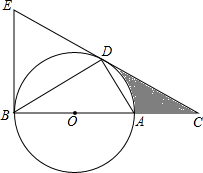 如图,D为⊙O上一点,点C在直径BA的延长线上,且∠CDA=∠CBD.
如图,D为⊙O上一点,点C在直径BA的延长线上,且∠CDA=∠CBD. 如图△ABC的顶点坐标分别为A(1,1),B(2,3),C(3,0).
如图△ABC的顶点坐标分别为A(1,1),B(2,3),C(3,0).