题目内容
20.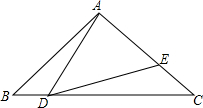 已知:如图,△ABC中,∠BAC=90°,AB=AC=1,点D是BC边上一个动点(不与B、C点重合),∠ADE=45°
已知:如图,△ABC中,∠BAC=90°,AB=AC=1,点D是BC边上一个动点(不与B、C点重合),∠ADE=45°(1)求证:△ABD∽△DCE.
(2)设BD=x,AE=y,求y关于x的函数关系式,并指出自变量x的取值范围.
(3)当点D在线段BC的什么位置时,AE的长度最短?请说明理由,并求出AE的最短长度是多少?
分析 (1)先判断△ABC为等腰直角三角形得到∠B=∠C=45°,再利用三角形内角和得到∠1+∠2=135°,利用平角定义得到∠2++∠3=135°,则∠1=∠3,于是可根据有两组角对应相等的两个三角形相似得到结论;
(2)由△ABD∽△DCE,对应边成比例及等腰直角三角形的性质可求出y与x的函数关系式;
(3)根据函数图象的顶点坐标可求出其最小值.
解答 (1)证明:∵∠BAC=90°,AB=AC=1,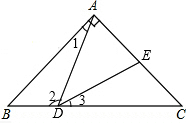
∴△ABC为等腰直角三角形,
∴∠B=∠C=45°,
∴∠1+∠2=180°-∠B=135°,
∵∠ADE=45°,
∴∠2+∠3=135°,
∴∠1=∠3,
∵∠B=∠C,
∴△ABD∽△DCE;
(2)解:由(1)得△ABD∽△DCE,
∴$\frac{BD}{EC}=\frac{AB}{CD}$,
∵∠BAC=90°,AB=AC=1,
∴BC=$\sqrt{2}$,DC=$\sqrt{2}$-x,EC=1-y,
∴$\frac{x}{1-y}=\frac{1}{\sqrt{2}-x}$,
∴y=x2-$\sqrt{2}$x+1(0<x$<\sqrt{2}$);
(3)解:∵y=x2-$\sqrt{2}$x+1=${(x-\frac{\sqrt{2}}{2})}^{2}$$+\frac{1}{2}$,
∴当x=$\frac{\sqrt{2}}{2}$时,y有最小值为$\frac{1}{2}$,
即BD=$\frac{\sqrt{2}}{2}$时,AE的最短长度是$\frac{1}{2}$.
点评 本题考查了相似三角形的判定及性质定理和等腰直角三角形的性质,综合运用相似三角形的判定及性质定理和二次函数的最值是解答此题的关键.

练习册系列答案
相关题目
 ,
, ,
, ,
, ,……则这列数的第6个数是
,……则这列数的第6个数是 B.
B.  C.
C.  D.
D. 
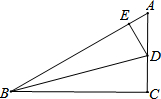 如图,在Rt△ABC中,∠C=90°,∠ABC=30°,BD是△ABC角平分线,求tan15°的值.(提示:过点D作DE⊥AB.垂足为点E.)
如图,在Rt△ABC中,∠C=90°,∠ABC=30°,BD是△ABC角平分线,求tan15°的值.(提示:过点D作DE⊥AB.垂足为点E.)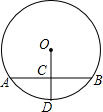 如图,已知⊙O的半径为5,弦AB的长为8,半径OD过AB的中点C,则CD的长为2.
如图,已知⊙O的半径为5,弦AB的长为8,半径OD过AB的中点C,则CD的长为2. 在直角坐标平面内,二次函数图象的顶点为A(1,-4),且过点B(3,0).
在直角坐标平面内,二次函数图象的顶点为A(1,-4),且过点B(3,0). 如图,把一张长方形的纸按图那样折叠后,B、D两点落在B′、D′点处,若得∠AOB′=80°,则∠B′OG的度数为50°.
如图,把一张长方形的纸按图那样折叠后,B、D两点落在B′、D′点处,若得∠AOB′=80°,则∠B′OG的度数为50°. 如图所示是由几个小立方块所搭的几何体的俯视图,小正方形中的数字表示在该位置小立方块的个数,请画出相应几何体的主视图和左视图.
如图所示是由几个小立方块所搭的几何体的俯视图,小正方形中的数字表示在该位置小立方块的个数,请画出相应几何体的主视图和左视图.