题目内容
5.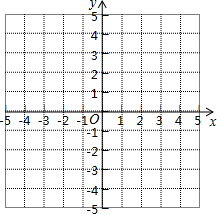 在直角坐标平面内,二次函数图象的顶点为A(1,-4),且过点B(3,0).
在直角坐标平面内,二次函数图象的顶点为A(1,-4),且过点B(3,0).(1)求该二次函数的解析式,并画出函数图象的草图;
(2)将该二次函数图象向右平移几个单位,可使平移后所得图象经过坐标原点?并直接写出平移后所得图象与x轴的另一个交点的坐标.
分析 (1)设二次函数的解析式为y=a(x-1)2-4,代入(3,0)根据待定系数法即可求得a;
(2)根据函数的图象即可求得.
解答 解:(1)∵二次函数图象的顶点为A(1,-4),
∴设二次函数的解析式为y=a(x-1)2-4,
∵二次函数图象过点B(3,0).
∴0=4a-4,
解得a=1,
∴该二次函数的解析式y=(x-1)2-4;
如图:
(2)由图象可知二次函数图象向右平移1个单位,可使平移后所得图象经过坐标原点,且与x轴的另一个交点坐标为(4,0).
点评 本题考查了待定系数法求二次函数的解析式以及函数图象的平移,根据平移规律“左加右减,上加下减”利用顶点的变化确定图形的变化是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
16.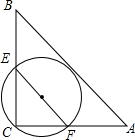 如图,Rt△ABC中,AC=4,AB=5,∠C=90°,经过点C且与边AB相切的圆与△ABC的边CB,CA分别相交于点E、F,线段EF长度的最小值为( )
如图,Rt△ABC中,AC=4,AB=5,∠C=90°,经过点C且与边AB相切的圆与△ABC的边CB,CA分别相交于点E、F,线段EF长度的最小值为( )
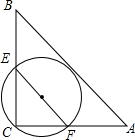 如图,Rt△ABC中,AC=4,AB=5,∠C=90°,经过点C且与边AB相切的圆与△ABC的边CB,CA分别相交于点E、F,线段EF长度的最小值为( )
如图,Rt△ABC中,AC=4,AB=5,∠C=90°,经过点C且与边AB相切的圆与△ABC的边CB,CA分别相交于点E、F,线段EF长度的最小值为( )| A. | 2.4 | B. | 2 | C. | 2.5 | D. | 2$\sqrt{2}$ |
13.使分式$\frac{x}{x+1}$有意义的条件是( )
| A. | x≠-1 | B. | x≠1 | C. | x≠0 | D. | x+1>0 |
17.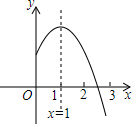 二次函数y=ax2+bx+c(a,b,c是常数,a≠0)图象的对称轴是直线x=1,其图象的一部分如图所示,对于下列说法:①abc<0;②a-b+c<0; ③3a+c<0; ④当y>0时,-1<x<3.其中正确的是( )
二次函数y=ax2+bx+c(a,b,c是常数,a≠0)图象的对称轴是直线x=1,其图象的一部分如图所示,对于下列说法:①abc<0;②a-b+c<0; ③3a+c<0; ④当y>0时,-1<x<3.其中正确的是( )
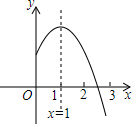 二次函数y=ax2+bx+c(a,b,c是常数,a≠0)图象的对称轴是直线x=1,其图象的一部分如图所示,对于下列说法:①abc<0;②a-b+c<0; ③3a+c<0; ④当y>0时,-1<x<3.其中正确的是( )
二次函数y=ax2+bx+c(a,b,c是常数,a≠0)图象的对称轴是直线x=1,其图象的一部分如图所示,对于下列说法:①abc<0;②a-b+c<0; ③3a+c<0; ④当y>0时,-1<x<3.其中正确的是( )| A. | ①、② | B. | ①、③ | C. | ①、②、③ | D. | ①、②、④ |
14.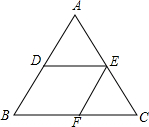 如图,DE∥BC,EF∥AC,则下列比例式中不正确的是( )
如图,DE∥BC,EF∥AC,则下列比例式中不正确的是( )
 如图,DE∥BC,EF∥AC,则下列比例式中不正确的是( )
如图,DE∥BC,EF∥AC,则下列比例式中不正确的是( )| A. | $\frac{AE}{AC}=\frac{AD}{AB}$ | B. | $\frac{AE}{EC}=\frac{BF}{FC}$ | C. | $\frac{AD}{BD}=\frac{BF}{FC}$ | D. | $\frac{BD}{AD}=\frac{BF}{FC}$ |

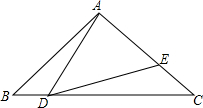 已知:如图,△ABC中,∠BAC=90°,AB=AC=1,点D是BC边上一个动点(不与B、C点重合),∠ADE=45°
已知:如图,△ABC中,∠BAC=90°,AB=AC=1,点D是BC边上一个动点(不与B、C点重合),∠ADE=45°