题目内容
11.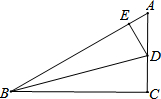 如图,在Rt△ABC中,∠C=90°,∠ABC=30°,BD是△ABC角平分线,求tan15°的值.(提示:过点D作DE⊥AB.垂足为点E.)
如图,在Rt△ABC中,∠C=90°,∠ABC=30°,BD是△ABC角平分线,求tan15°的值.(提示:过点D作DE⊥AB.垂足为点E.)
分析 设AC=a,在Rt△ABC中,∠C=90°,∠ABC=30°,利用∠ABC的正切可表示出BC=$\sqrt{3}$a,过点D作DE⊥AB.垂足为点E,如图,根据角平分线性质得DE=DC,∠DBC=15°,设CD=x,则DE=x,AD=a-x,在Rt△ADE,根据∠A的正弦得到DE=$\frac{\sqrt{3}}{2}$AD,即x=$\frac{\sqrt{3}}{2}$(a-x),所以x=$\frac{\sqrt{3}a}{2+\sqrt{3}}$,在Rt△BDC中,利用正切的定义可求出tan15°的值.
解答 解:设AC=a,
在Rt△ABC中,∠C=90°,∠ABC=30°,
∵tan∠ABC=$\frac{AC}{BC}$,
∴BC=$\frac{a}{tan30°}$=$\sqrt{3}$a,
过点D作DE⊥AB.垂足为点E,如图,
∵BD是△ABC角平分线,
∴DE=DC,∠DBC=15°,
设CD=x,则DE=x,AD=a-x,
在Rt△ADE,∵sinA=$\frac{DE}{AD}$=sin60°=$\frac{\sqrt{3}}{2}$,
∴DE=$\frac{\sqrt{3}}{2}$AD,即x=$\frac{\sqrt{3}}{2}$(a-x),
∴x=$\frac{\sqrt{3}a}{2+\sqrt{3}}$,
在Rt△BDC中,tan∠DBC=$\frac{DC}{BC}$=$\frac{\frac{\sqrt{3}a}{2+\sqrt{3}}}{\sqrt{3}a}$=$\frac{1}{2+\sqrt{3}}$=2-$\sqrt{3}$,
即tan15°=2-$\sqrt{3}$.
点评 本题考查了解直角三角形:在直角三角形中,由已知元素求未知元素的过程就是解直角三角形.解决本题的关键是灵活运用勾股定理和锐角三角函数的定义.

 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案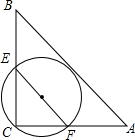 如图,Rt△ABC中,AC=4,AB=5,∠C=90°,经过点C且与边AB相切的圆与△ABC的边CB,CA分别相交于点E、F,线段EF长度的最小值为( )
如图,Rt△ABC中,AC=4,AB=5,∠C=90°,经过点C且与边AB相切的圆与△ABC的边CB,CA分别相交于点E、F,线段EF长度的最小值为( )| A. | 2.4 | B. | 2 | C. | 2.5 | D. | 2$\sqrt{2}$ |
 ,3,5,6,5,则这组数据的中位数是______;
,3,5,6,5,则这组数据的中位数是______; .
.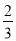 ,
,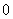 ,
, 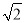 ,
,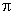 ,
, 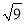 中,无理数有( )
中,无理数有( )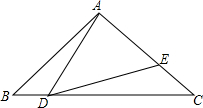 已知:如图,△ABC中,∠BAC=90°,AB=AC=1,点D是BC边上一个动点(不与B、C点重合),∠ADE=45°
已知:如图,△ABC中,∠BAC=90°,AB=AC=1,点D是BC边上一个动点(不与B、C点重合),∠ADE=45°