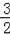题目内容
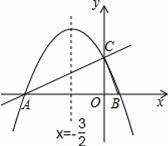
如图,▱ABCD的对角线AC、BD相交于点O,AE=CF.
(1)求证:△BOE≌△DOF;
(2)若BD=EF,连接DE、BF,判断四边形EBFD的形状,无需说明理由.


【考点】平行四边形的性质;全等三角形的判定与性质.
【专题】证明题.
【分析】(1)先证出OE=OF,再由SAS即可证明△BOE≌△DOF;
(2)由对角线互相平分证出四边形EBFD是平行四边形,再由对角线相等,即可得出四边形EBFD是矩形.
【解答】(1)证明:∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD,
∵AE=CF,∴OE=OF,
在△BOE和△DOF中,
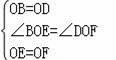
 ,
,
∴△BOE≌△DOF(SAS);
(2)解:四边形EBFD是矩形;理由如下:
∵OB=OD,OE=OF,
∴四边形EBFD是平行四边形,
∵BD=EF,
∴四边形EBFD是矩形.
【点评】本题考查了平行四边形的性质与判定、全等三角形的判定与性质、矩形的判定;熟练掌握平行四边形的性质,并能进行推理论证是解决问题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目

 ,1,3的不透明卡片,它们除数字不同外其余全部相同.现将它们背面朝上,洗匀后从中任取一张,将该卡片上的数字记为a,则使关于x的分工方程
,1,3的不透明卡片,它们除数字不同外其余全部相同.现将它们背面朝上,洗匀后从中任取一张,将该卡片上的数字记为a,则使关于x的分工方程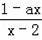
 +2=
+2=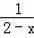
 有整数解的概率是 .
有整数解的概率是 .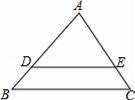


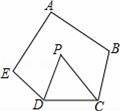
 x+2与x轴交于点A,与y轴交于点C.抛物线y=ax2+bx+c的对称轴是x=﹣
x+2与x轴交于点A,与y轴交于点C.抛物线y=ax2+bx+c的对称轴是x=﹣