Question

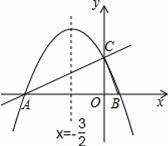
如图，在平面直角坐标系xOy中，直线y=x+2与x轴交于点A，与y轴交于点C．抛物线y=ax²+bx+c的对称轴是x=﹣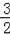且经过A、C两点，与x轴的另一交点为点B．

（1）①直接写出点B的坐标；②求抛物线解析式．

（2）若点P为直线AC上方的抛物线上的一点，连接PA，PC．求△PAC的面积的最大值，并求出此时点P的坐标．

（3）抛物线上是否存在点M，过点M作MN垂直x轴于点N，使得以点A、M、N为顶点的三角形与△ABC相似？若存在，求出点M的坐标；若不存在，请说明理由．

Answer 1

【考点】二次函数综合题．

【专题】压轴题．

【分析】（1）①先求的直线y=x+2与x轴交点的坐标，然后利用抛物线的对称性可求得点B的坐标；②设抛物线的解析式为y=y=a（x+4）（x﹣1），然后将点C的坐标代入即可求得a的值；

（2）设点P、Q的横坐标为m，分别求得点P、Q的纵坐标，从而可得到线段PQ=m²﹣2m，然后利用三角形的面积公式可求得S_△PAC=×PQ×4，然后利用配方法可求得△PAC的面积的最大值以及此时m的值，从而可求得点P的坐标；

（3）首先可证明△ABC∽△ACO∽△CBO，然后分以下几种情况分类讨论即可：①当M点与C点重合，即M（0，2）时，△MAN∽△BAC；②根据抛物线的对称性，当M（﹣3，2）时，△MAN∽△ABC； ④当点M在第四象限时，解题时，需要注意相似三角形的对应关系．

【解答】解：（1）①y=当x=0时，y=2，当y=0时，x=﹣4，

∴C（0，2），A（﹣4，0），

由抛物线的对称性可知：点A与点B关于x=﹣对称，

∴点B的坐标为1，0）．

②∵抛物线y=ax²+bx+c过A（﹣4，0），B（1，0），

∴可设抛物线解析式为y=a（x+4）（x﹣1），

又∵抛物线过点C（0，2），

∴2=﹣4a

∴a=

∴y=x²x+2．

（2）设P（m， m²m+2）．

过点P作PQ⊥x轴交AC于点Q，

∴Q（m， m+2），

∴PQ=m²m+2﹣（m+2）

=m²﹣2m，

∵S_△PAC=×PQ×4，

=2PQ=﹣m²﹣4m=﹣（m+2）²+4，

∴当m=﹣2时，△PAC的面积有最大值是4，

此时P（﹣2，3）．

（3）在Rt△AOC中，tan∠CAO=在Rt△BOC中，tan∠BCO=，

∴∠CAO=∠BCO，

∵∠BCO+∠OBC=90°，

∴∠CAO+∠OBC=90°，

∴∠ACB=90°，

∴△ABC∽△ACO∽△CBO，

如下图：

①当M点与C点重合，即M（0，2）时，△MAN∽△BAC；

②根据抛物线的对称性，当M（﹣3，2）时，△MAN∽△ABC；

③当点M在第四象限时，设M（n， n²n+2），则N（n，0）

∴MN=n²+n﹣2，AN=n+4

当时，MN=AN，即n²+n﹣2=（n+4）

整理得：n²+2n﹣8=0

解得：n₁=﹣4（舍），n₂=2

∴M（2，﹣3）；

当时，MN=2AN，即n²+n﹣2=2（n+4），

整理得：n²﹣n﹣20=0

解得：n₁=﹣4（舍），n₂=5，

∴M（5，﹣18）．

综上所述：存在M₁（0，2），M₂（﹣3，2），M₃（2，﹣3），M₄（5，﹣18），使得以点A、M、N为顶点的三角形与△ABC相似．

【点评】本题主要考查的是二次函数与相似三角形的综合应用，难度较大，解答本题需要同学们熟练掌握二次函数和相似三角形的相关性质．