题目内容
7.已知抛物线y=ax2+bx+c经过(-1,0),(0,-3),(2,3)三点.(1)求这条抛物线的表达式.
(2)写出抛物线的开口方向、对称轴和顶点坐标.
分析 (1)将三点代入y=ax2+bx+c,得到三元一次方程组,解这个方程组得a、b、c的值,得到抛物线的解析式.
(2)把解析式化成顶点式,根据抛物线的性质即可求得.
解答 解:(1)由题意得$\left\{\begin{array}{l}{a-b+c=0}\\{c=-3}\\{4a+2b+c=3}\end{array}\right.$,
解得$\left\{\begin{array}{l}{a=2}\\{b=-1}\\{c=-3}\end{array}\right.$.
所以这个抛物线的表达式为y=2x2-x-3.
(2)y=2x2-x-3=2(x-$\frac{1}{4}$)-$\frac{25}{8}$,
所以抛物线的开口向上,对称轴为x=$\frac{1}{4}$,顶点坐标为($\frac{1}{4}$,-$\frac{25}{8}$)
点评 本题主要考查了待定系数法求二次函数的解析式以及二次函数的性质,熟练掌握待定系数法是本题的关键.

练习册系列答案
相关题目
2. 如图,点A、B、C在⊙O上,∠OBC=50°,则∠A的度数等于( )
如图,点A、B、C在⊙O上,∠OBC=50°,则∠A的度数等于( )
 如图,点A、B、C在⊙O上,∠OBC=50°,则∠A的度数等于( )
如图,点A、B、C在⊙O上,∠OBC=50°,则∠A的度数等于( )| A. | 20° | B. | 40° | C. | 50° | D. | 100° |
19.观察下列图形,是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
17.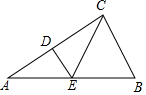 在△ABC中,DE垂直平分AC交AB于点E,∠A=30°,∠BCE=50°,则∠B=( )
在△ABC中,DE垂直平分AC交AB于点E,∠A=30°,∠BCE=50°,则∠B=( )
 在△ABC中,DE垂直平分AC交AB于点E,∠A=30°,∠BCE=50°,则∠B=( )
在△ABC中,DE垂直平分AC交AB于点E,∠A=30°,∠BCE=50°,则∠B=( )| A. | 60° | B. | 70° | C. | 80° | D. | 50° |
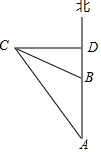 如图,下午2时一艘轮船从A处向正北方向航行,5时达到B处,继续航行到达D处时发现,灯塔C恰好在正西方向,从A处、B处望灯塔C的角度分别是∠A=30°,∠DBC=60°,已知轮船的航行速度为24海里/时,求AD的长度.
如图,下午2时一艘轮船从A处向正北方向航行,5时达到B处,继续航行到达D处时发现,灯塔C恰好在正西方向,从A处、B处望灯塔C的角度分别是∠A=30°,∠DBC=60°,已知轮船的航行速度为24海里/时,求AD的长度.