题目内容
17．
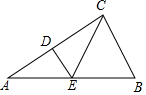在△ABC中，DE垂直平分AC交AB于点E，∠A=30°，∠BCE=50°，则∠B=（ ）| A． | 60° | B． | 70° | C． | 80° | D． | 50° |
分析 根据线段垂直平分线的性质得到EA=EC，根据等腰三角形的性质求出∠ECA=∠A=30°，根据三角形的外角的性质求出∠BEC，根据三角形内角和定理计算即可．
解答 解：∵DE垂直平分AC，
∴EA=EC，
∴∠ECA=∠A=30°，
∴∠BEC=∠ECA+∠A=60°，
∴∠B=180°-∠BEC-∠BCE=70°，
故选：B．
点评 本题考查的是线段垂直平分线的性质、三角形内角和定理的应用，掌握线段的垂直平分线上的点到线段的两个端点的距离相等是解题的关键．
练习册系列答案
相关题目
8．连续抛掷一枚质地均匀的硬币三次，有“两次正面朝上一次反面朝上”的概率是（ ）
| A． | $\frac{1}{8}$ | B． | $\frac{1}{4}$ | C． | $\frac{3}{8}$ | D． | $\frac{1}{2}$ |
如图，已知AB=CD，AE=DF，BF=CE，求证∠B=∠C．
2．下列命题是真命题的是（ ）
| A． | 周长相等的两个三角形全等 | |
| B． | 等底等高的两个三角形全等 | |
| C． | 有两边和一角对应相等的两个三角形全等 | |
| D． | 有一条直角边和斜边上的高对应相等的两个直角三角形全等 |
6．
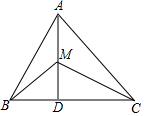如图所示，已知△ABC中，AB=6，AC=9，AD⊥BC于D，M为AD上任一点，则MC2-MB2等于（ ）
如图所示，已知△ABC中，AB=6，AC=9，AD⊥BC于D，M为AD上任一点，则MC2-MB2等于（ ）| A． | 15 | B． | 45 | C． | 35 | D． | 25 |
