题目内容
阅读下列材料,并解决下面的问题.
我们知道一般地,加减运算是互逆运算,乘除运算也是互逆运算;其实乘方运算也有逆运算;如我们规定式子23=8可以变形为log28=3,log525=2也可以变形为52=25.在式子23=8中,3叫做以2为底8的对数,记为log2 8.一般地,若an=b(a>0且a≠1,b>0),则n叫做以a为底b的对数,记为logab(即logab=n).
根据上面的规定,请解决下列问题:
(1)计算:log3 1= ,log1025+log104= ;
(2)已知x=log32,请你用x的代数式来表示y(其中y=log372).(请写出必要的过程)
我们知道一般地,加减运算是互逆运算,乘除运算也是互逆运算;其实乘方运算也有逆运算;如我们规定式子23=8可以变形为log28=3,log525=2也可以变形为52=25.在式子23=8中,3叫做以2为底8的对数,记为log2 8.一般地,若an=b(a>0且a≠1,b>0),则n叫做以a为底b的对数,记为logab(即logab=n).
根据上面的规定,请解决下列问题:
(1)计算:log3 1=
(2)已知x=log32,请你用x的代数式来表示y(其中y=log372).(请写出必要的过程)
考点:幂的乘方与积的乘方
专题:阅读型,新定义
分析:(1)先认真阅读题目,得出3x=1,求出x即可;得出log1025+log104=log10100,求出即可;
(2)先变形得出y=log372,再求出即可.
(2)先变形得出y=log372,再求出即可.
解答:解:(1)log31=0,log1025+log104=log10100=2,
故答案为:0,2;
(2)∵x=log32,
∴y=log372
=log38+log39
=3log32+2
=3x+2.
故答案为:0,2;
(2)∵x=log32,
∴y=log372
=log38+log39
=3log32+2
=3x+2.
点评:本题考查了幂的乘方和积的乘方的应用,注意:一般地,若an=b(a>0且a≠1,b>0),则n叫做以a为底b的对数,记为logab(即logab=n).

练习册系列答案
 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
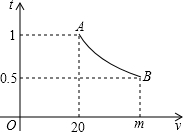 一辆汽车匀速通过某段公路,所需时间t(h)与行驶速度v(km/h)满足函数关系:t=
一辆汽车匀速通过某段公路,所需时间t(h)与行驶速度v(km/h)满足函数关系:t=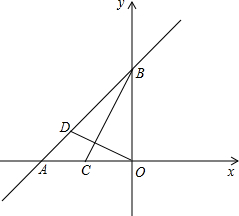 如图,在平面直角坐标系中,直线y=x+4与x轴交于点A,与y轴交于点B,点C(-2,0).
如图,在平面直角坐标系中,直线y=x+4与x轴交于点A,与y轴交于点B,点C(-2,0).